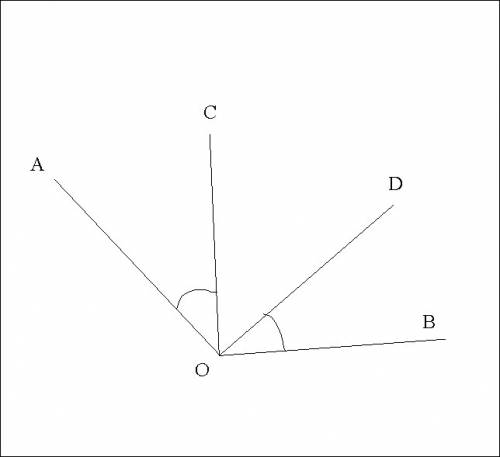
Дано:
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90°; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
первое число дает остаток 1 при делении на 4
значит куб первого числа при делении на 4 даст такой же остаток как и 1 в кубе, т.е как число 1*1*1=1
число 1 при делении на 4 дает остаток 1
итого куб первого числа при делении на 4 даст остаток 1
второе число дает остаток 3 при делении на 4
значит куб второго числа при делении на 4 даст такой же остаток как и 3 в кубе, т.е. как число 3*3*3=27
число 27 при делении на 4 дает остаток 3
сумма кубов первого и второго чисел при делении на 4 даст такой же остаток какой даст при делении на 4 сумма остатков чисел при делении на 4, т.е. как число 1+3=4,
так как 4 при делении на 4 дает остаток 0, то
сумма кубов этих чисел кратна 4
----------------------------------
второй
так как первое число при делении на 4 дает остаток 1, то его можно записать в виде 4n+1, где n - некоторое целое число
аналогично второе можно записать в виде 4k+3, где k - некоторое целое число
сумма кубов этих чисел
а значит сумма кубов делится нацело на 4. Доказано