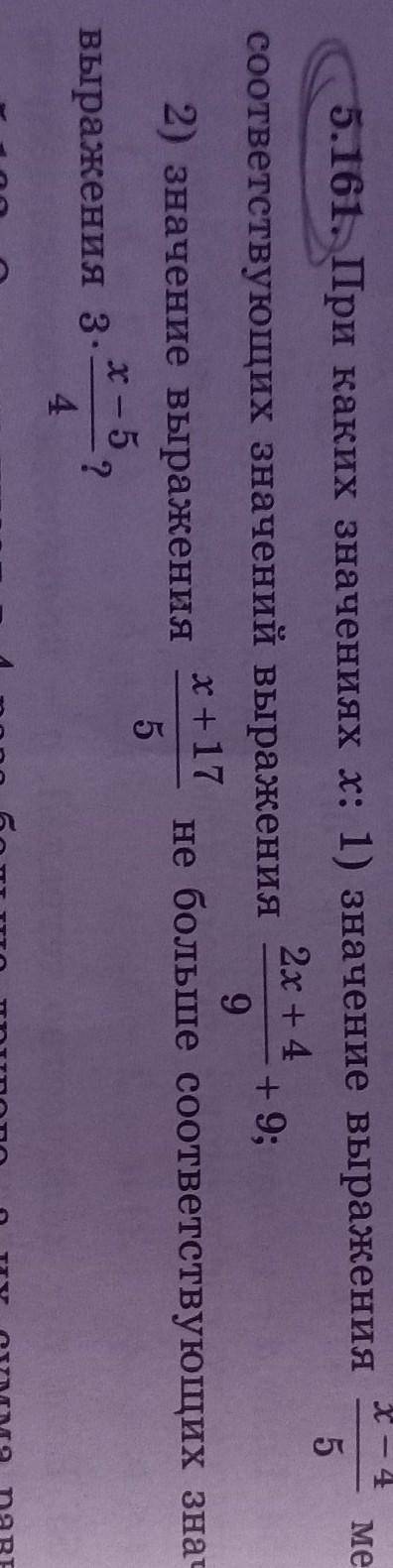
Нет такой арифметической прогрессии
Объяснение:
Нужно знать:
1) Формула n-го члена арифметической прогрессии
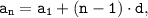
где a₁ - первый член, d - разность арифметической прогрессии.
2) Сумма первых n членов арифметической прогрессии (аn) обозначается Sn:
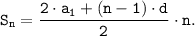
Решение. Известно
a₃-a₁=8, a₂+a₄=14, Sn=111.
Так как
a₃-a₁=a₁+2·d-a₁=2·d,
то определим разность d:
2·d=8 или d=4.
Из второго равенства находим a₁:
a₂+a₄=a₁+d+a₁+3·d=2·a₁+4·d=2·a₁+4·4=2·a₁+16=14, то
2·a₁=14-16 или 2·a₁= -2 или a₁= -1.
Из второго равенства находим число членов арифметической прогрессии в сумме:
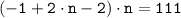
2·n²-3·n-111=0
D=(-3)²-4·2·(-111)=9+888=897
Так как √897 - иррациональное число, то при таких условиях нет решения.
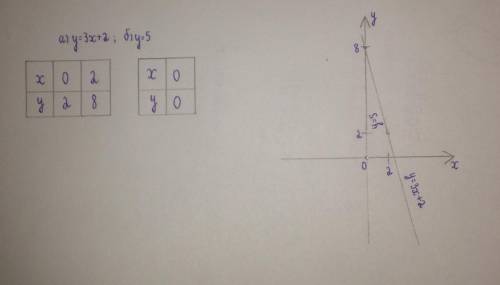
График функции, заданной формулой у=kx+b – является линейной функцией. Графиком линейной функции является прямая. Для построения графика найдём координаты двух точек:
х=0, то у=2, так как 3×0+2, то будет 2.
х=2, то у=8, так как 3×2+2, получится 8.
График функции, заданной формулой у=kx – является прямой пропорциональностью. Графиком прямой пропорциональности является прямая, проходящая через начало координат. Для построения графика найдём координаты ещё одной точки:
х=0, то у=0, так как 5×0, будет 0.
В решении.
Объяснение:
1) (х - 4)/5 < (2х + 4)/9 + 9
Умножить все части неравенства на 45, чтобы избавиться от дробного выражения:
9*(х - 4) < 5*(2x + 4) + 45*9
9x - 36 < 10x + 20 + 405
9x - 10x < 425 + 36
-х < 461
x > -461
При х > -461 первое выражение меньше второго.
2) (х + 17)/5 = 3(х - 5)/4
Умножить все части уравнения на 20, чтобы избавиться от дробного выражения:
4*(х + 17) = 5*3(х - 5)
4х + 68 = 15х - 75
4х - 15х = -75 - 68
-11х = -143
х = -143/-11
х = 13.
При х = 13 первое выражение не больше второго (равно ему).