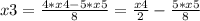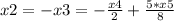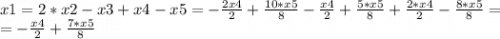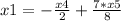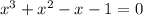
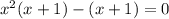
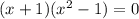
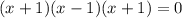
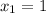
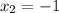
заменой
x в квад=y
y в квадр + у -2 =0
у1=1
у2=-2
x=+-1
ответ:+-1
Вспомним,что полный круг-360 градусов. Каждая четверть-90°. Тогда:
1) 179° - 2 четверть ( не хватает 1° до 180°)
2)325° - 4 четверть (не хватает 35° до 360°-полного круга)
3)-150° - 3 четверть (идем в отрицательном направлении ,не хватает -30° до -180°)
4)-10° - 4 четверть(идем в отрицательном направлении по часовой стрелке)
5) 800° - 1 четверть (в положительном направлении, 720°- это 2 полных круга,можно отбросить, добавляем еще 80° и остаемся еще в 1 четверти)
6) 10000° - 4 четверть ( 27 полных круга и еще 280° , 280° - это полкруга(180) и еще 100°,оказываемся в 4 четверти)
Объяснение:
Первая система линейных уравнений:
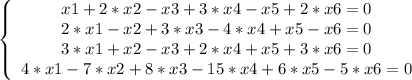
1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.
1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.
1-ое уравнение умножаем на -4 и складываем с 4-ым уравнением.
Получаем нули при x1 во всех уравнениях, кроме 1-го:
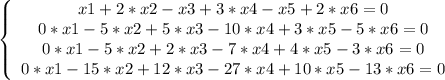
2-ое уравнение умножаем на -1 и складываем с 3-им уравнением.
2-ое уравнение умножаем на -3 и складываем с 4-ым уравнением.
Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:
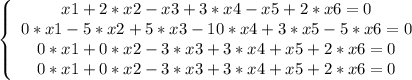
3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:
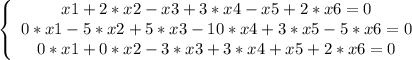
Получилась система, из которой можно получить фундаментальное решение:
x4, x5, x6 ∈ R
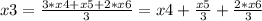
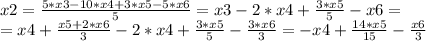
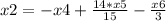
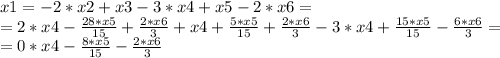
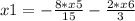
Вторая система решается точно также.
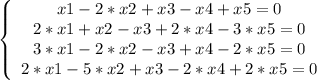
1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.
1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.
1-ое уравнение умножаем на -2 и складываем с 4-ым уравнением.
Получаем нули при x1 во всех уравнениях, кроме 1-го:
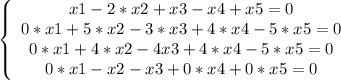
4-ое уравнение ставим 2-ым, от этого система не меняется:
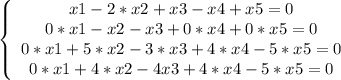
2-ое уравнение умножаем на 5 и складываем с 3-им уравнением.
2-ое уравнение умножаем на 4 и складываем с 4-ым уравнением.
Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:
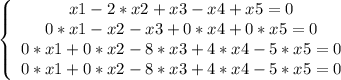
3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:
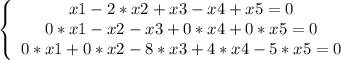
Получилась система, из которой можно получить фундаментальное решение:
x4, x5 ∈ R