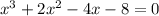
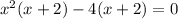
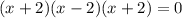

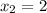
x^3+2x^2-4x-8=0
x^3-4x+2x^2-8=0
вынесем х в первых двух одночленах и 2 в след. двух. затем сгруппируем
(x^2-4)(x+2)=0
разложим на множители:
(x-2)(x+2)(x+2)=0
(x-2)(x+2)^2=0
(x-2)=0 или (x+2)^2=0 { произведение двух чисел равно нулю,
x-2=0 или х+2=0 когда один из множителей
х=2 или х=-2 равен нулю}
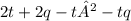
Ну, решать здесь нечего, так как это ни задача, ни неравенство, ни даже уравнение. Здесь можно только упростить, разложить на множители.
Видим, что у первый двух слагаемых есть общий множитель 2. А у вторых двух -t. Объединим одночлены в группы и вынесем общее. Если что, вынести общий множитель - значит разделить каждое слагаемое на него. Например, у 2t и 2q общий множитель 2. Чтобы вынести его за скобку, мы должны 2t поделить на 2 и 2q поделить на 2. То есть: 2t+2q=2(t-q). Можем себя проверить, умножив двойку на эту скобку. Получим тоже самое: 2*t+2*q. Таким образом:
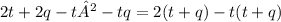
У t и q общее было - t. Мы разделили - t² и - tq на - t, получили t и q.
Теперь можем увидеть, что t+q - это общий множитель у получившихся слагаемых. Можем его тоже вынести, поделив 2(t+q) на t+q и - t(t+q) тоже делим на t+q. Получаем:
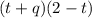
Это максимально упрощённое выражение.
Такое упрощение называют разложением многочлена на множители.
15*(X+3)*(X-5) + 10*(X+2)*(X-5) +6*(X+2)*(X+3) \ 30*(X+2)*(X+3)*(X-5) = 2
15*(X^2-2X-15) +10*(X^2-3X-10) +6*(X^2+5X+6) = 60*(X+2)*(X+3)*(X-5)
15X^2 - 30X - 225 + 10X^2 - 30X - 100 +6X^2 +30X + 36 =
= 31X^2 - 30X - 289
60*(X+2)*(X+3)*(X-5) = 60*(X^2+5X+6)*(X-5) = 60*(X^3 - 19X -30) = 60X^3 - 1140X - 1800
31X^2 - 30X - 289 = 60X^3 - 1140X - 1800
60X^3 - 31X^2 - 1110X - 1511 = 0
Берём производную:
180X^2 - 62X - 1110X = 0
2*(90X^2 - 31X - 555) = 0
D = 961 - 4*90*(-555) = 961 + 199800=200761 V D = 448
X1 = 31 + 448 \ 180 = 2.6
X2 = 31 - 448 \ 180 = - 417\180 = - 2.3