AE : CE = 9 : 5
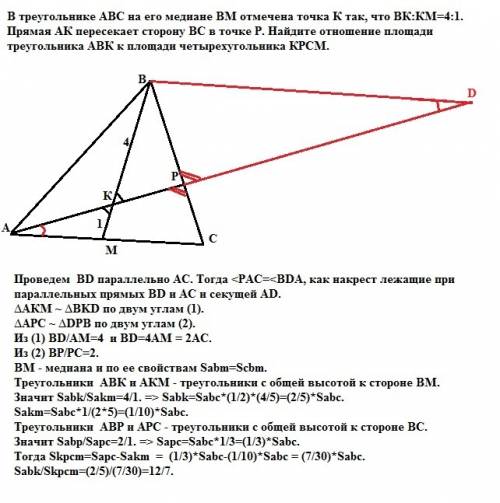
Рассмотрим треугольники AKE и ABC. У них \angle A∠A - общий. \angle AKE=\angle ABC∠AKE=∠ABC как соответственные. Следовательно, треугольники AKE и АВС подобны (по двум углам). Из подобия треугольников следует пропорциональность соответствующих сторон
\dfrac{AE}{AC}=\dfrac{AK}{AB}~~\Rightarrow~~~ \dfrac{9}{14}=\dfrac{AK}{42}~~\Rightarrow~~ \boxed{AK=27}
AC
AE
=
AB
AK
⇒
14
9
=
42
AK
⇒
AK=27
Аналогично, \Delta PEC\sim \Delta ABCΔPEC∼ΔABC (по двум углам).
\dfrac{CE}{AC}=\dfrac{PE}{AB}~~\Rightarrow~~\dfrac{5}{14}=\dfrac{PE}{42}~~\Rightarrow~~ \boxed{PE=15}
AC
CE
=
AB
PE
⇒
14
5
=
42
PE
⇒
PE=15
\dfrac{BC}{PC}=\dfrac{AB}{PE}~~\Rightarrow~~~\dfrac{BP+PC}{PC}=\dfrac{42}{15}~~\Rightarrow~~ \boxed{\dfrac{BP}{PC}=\dfrac{9}{5}}
PC
BC
=
PE
AB
⇒
PC
BP+PC
=
15
42
⇒
PC
BP
=
5
9
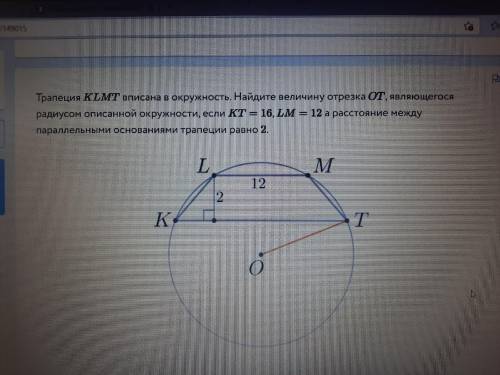
Опустим перпендикуляр из точки О на LM в точку В.
Пересечение с КТ - точка А.
Радиус описанной окружности R.
Примем ОА = х, ОВ = х + 2.
По Пифагору х² + (16/2)² = R².
Также (х + 2)² + (12/2)² = R².
Приравняем х² + 64 = х² + 4x + 4 + 36.
Получаем 4х = 24, откуда х = 24/4 = 6.
Тогда радиус R = √(6² + 8²) = √(36 + 64) = √100 = 10.
ответ: радиус равен 10.