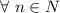База индукции: Квадрата два на два, у которого отсутствует одна угловая клетка, естественным образом разбивается на уголки из трёх клеток (Рис. 3).
Индукционное предположение: Квадрат на с отсутствующей угловой клеткой можно разбить на уголки из трёх клеток.
Индукционный шаг: Пусть есть квадрат на , разобъем его на четыре части так, как указано на Рис. 1. Получим четыре квадрата на и четыре незаполненных клетки, три из которых можно заполнить уголком (на Рис. 2 синий). Квадраты же на без угловных клеток мы можем заполнить согласно индукционному предположению.
Вывод: Квадрат на , без угловой клетки можно разбить на уголки из трёх клеток для
Выпишем последовательность чисел, которые делятся на 3: 3, 6, 9, ..., 150 - это арифметическая прогрессия, где: => n=50 шт. - это сумма всех натуральных чисел, не превосходящих 150, делящихся на 3.
Из последовательности нужно исключить числа, делящиеся на 4: 4, 8, 12,...,148 - арифметическая прогрессия, где: => k=37 шт. - это сумма всех натуральных чисел, не превосходящих 150, делящихся на 4.
Сумма натуральных чисел, не превосходящих 150, делящихся на 3 и не делящихся на 4, равна: S=3825-2812=1013
База индукции: Квадрата два на два, у которого отсутствует одна угловая клетка, естественным образом разбивается на уголки из трёх клеток (Рис. 3).
Индукционное предположение: Квадрат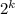 на
на 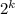 с отсутствующей угловой клеткой можно разбить на уголки из трёх клеток.
с отсутствующей угловой клеткой можно разбить на уголки из трёх клеток.
Индукционный шаг: Пусть есть квадрат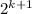 на
на 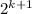 , разобъем его на четыре части так, как указано на Рис. 1. Получим четыре квадрата
, разобъем его на четыре части так, как указано на Рис. 1. Получим четыре квадрата 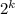 на
на 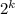 и четыре незаполненных клетки, три из которых можно заполнить уголком (на Рис. 2 синий). Квадраты же
и четыре незаполненных клетки, три из которых можно заполнить уголком (на Рис. 2 синий). Квадраты же 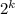 на
на 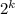 без угловных клеток мы можем заполнить согласно индукционному предположению.
без угловных клеток мы можем заполнить согласно индукционному предположению.
Вывод: Квадрат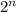 на
на 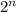 , без угловой клетки можно разбить на уголки из трёх клеток для
, без угловой клетки можно разбить на уголки из трёх клеток для