Question

№1 Упростите выражение (х+9)(х+1)-(х-7)(х+4) при х=-1
№2решите уравнение
(х+6)(х-1)-(х+3)(х-4)
№3Найдите четыре последовательных целых числа, таких чтобы произведение четвёртого и третьего из этих чисел на 10 больше произведения второго и первого
​

Answer 1

1) (x+9)(x+1)-(x-7)(x+4)=(1+9)(1+1)-(1-7)(1+4)=10*2-(-6)*5=20+30=50

3)пусть последовательные числа n-1, n, n+1,n+2  

(n - 1)n +10 = (n+1)(n + 2)

n² - n + 10 = n² + 3n + 2

4n = 8

n = 2

n-1=2-1=1

2

3

4

Объяснение:

2) (x+6)(x-1)-(x+3)(x-4)=0

x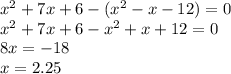$x^{2} +7x+6-(x^{2} -x-12)=0\\x^{2} +7x+6-x^{2} +x+12=0\\8x=-18\\x=2.25$если выражение равно 0 то решается так