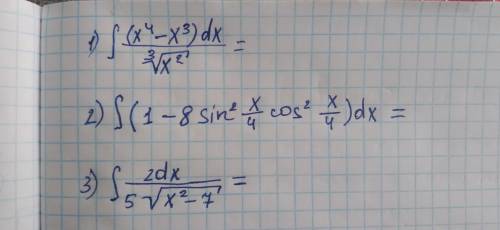
Прямая,все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это перпендикуляр к середине отрезка АВ.
Уравнение АВ: (х - 4)/(8 - 4) =(у - 2)/(8 - 2).
(х - 4)/4 =(у - 2)/6) или (х - 4)/2 =(у - 2)/3.
Или в общем виде Ах + Ву + С = 0.
3х - 12 = 2у - 8,
3х - 2у - 4 = 0. Здесь А = 3, В = -2.
Перпендикулярная прямая имеет вид -Вх + Ау + С1 = 0.
Для определения коэффициента С1 надо подставить координаты точки, принадлежащей этой прямой.
Такая точка - середина АВ (точка Д).
Д = (1/2)(A(4;2) + B(8;8))/2 = (6; 5). Подставляем:
2*6 + 3*5 + С1 = 0,
С1 = -12 - 15 = -27.
ответ: уравнение прямой, все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это 2х + 3у - 27 = 0.
2) -1 целая 1\7*(4\5+19\20)*(6 целых 5\6+4 целых 2\3) = -8/7*(16/20+19/20)*(41/6+14/3) = -8/7*35/20*(41/6+28/6) = -10/5*69/6 = -2*69/6 = -69/3 = -23
3) (6 целых 3\8-2целых 3\4)*(-4)+7\18*9 = (51/8-11/4)*(-4)+7/2 = (51/8-22/8)*(-4)+7/2 = 29/8*(-4)+7/2 = -29/2+7/2 = -22/2 = -11
4) 9 целых 1\6:(4 целых 1\3-8)+24*3\8 = 55/6:(13/3-24/3)+9 = 55/6:(-11/3)+9 = 55/6*(-3/11)+9 = -5/2+9 = 6,5