Повернём квадрат так, чтобы наименьшее из записанных чисел оказалось в правом нижнем углу. Пусть оно равно x. Тогда в левом нижнем углу и правом верхнем углу должны быть записаны числа вида ax и bx, где a и b – некоторые натуральные числа, для определённости a > b, иначе можно отразить квадрат относительно диагонали. Число в левом верхнем углу не может делиться на x (иначе на диагонали будет пара, в которой одно число делится на другое), тогда это какой-то общий делитель чисел ax и bx, обозначим его как d.
Заметим, что x ≥ 2 (иначе будет делящаяся пара чисел на диагонали); d ≥ x + 1 (по предположению, x – наименьшее число, и d не делится на x); bx ≥ 2d ≥ 2x + 2 (bx делится на d и bx > d, иначе, если bx = d, d будет делиться на x); ax > bx ≥ 3d ≥ 3x + 3. Значит, сумма всех записанных чисел не меньше x + 6d = x + d + 2d + 3d ≥ x + (x + 1) + (2x + 2) + (3x + 3) = 7x + 6.
Если в квадрате расставлены числа 2, 6, 12 и 3, то такая расстановка удовлетворяет условию и сумма чисел равна 23. Если какая-то существует какая-то подходящая расстановка с не большей суммой чисел, то 7x + 6 ≤ 23, x ≤ 2 (отсюда x = 2) и x + 6d = 2 + 6d ≤ 23, d ≤ 3 (отсюда d = 3). При этом ax и bx должны одновременно делиться на x и d, то есть на 2 и 3, значит, они делятся на 2 • 3 = 6, откуда bx ≥ 6, ax ≥ 6 • 2 = 12, и сумма чисел не меньше 23.
ответ. 23
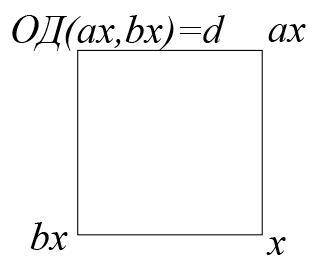
6
Объяснение:
a; b - катеты, см.
(a+4) - гипотенуза, см.
Система уравнений:
a+b+(a+4)=24; 2a+b=24-4; 2a+b=20; b=20-2a
a²+b²=(a+4)²; a²+b²=a²+8a+16; b²=8a+16
(20-2a)²=8a+16
400-80a+4a²=8a+16 |4
a²-20a+100-2a-4=0
a²-22a+96=0; D=484-384=100
a₁=(22-10)/2=12/2=6 см; b₁=20-2·6=20-12=8 см
a₂=(22+10)/2=32/2=16 см; b₂=20-2·16=20-32=-12 - ответ не подходит по смыслу.
Следовательно, a=6 см - меньший катет прямоугольного треугольника.