Решаем по данному условию.
30%=0,3
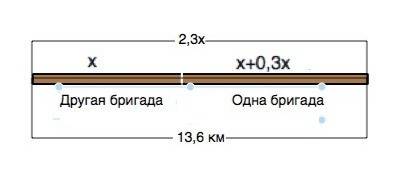
Примем участок, который отремонтировала вторая бригада, за х.
Тогда первая бригада отремонтировала на 0,3 больше от того, что сделала вторая бригада, т.е. от х. Выработка первой бригады 1,3 х.
Вместе они отремонтировали 13,6 км дороги..
Составим уравнение:
х+1,3х=13,6
2,3х=13,6
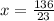 (км)
(км)
Первая бригада отремонтировала
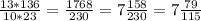 км.
км.
Проверка:
(1360+1768)/230=3128/230=13,6
Если нужны ответы в десятичных дробях, то после округления:
вторая бригада отремонтировала 5,913 км, первая 7,687 км
————
Получились бы другие числа, будь условие несколько иным.
Если бы участок, который отремонтировала одна из них, оказался на 30% короче участка, который отремонтировала другая бригада.
Тогда ответы стали бы более приятными на вид:
х+0,7х=13,6
откуда х=8 (км)- одна бригада.
и 0,7х=5,6 (км )- другая бригада
Пусть сторона квадрата х см, тогда длина прямоугольника (3х) см, а ширина прямоугольника - (х - 5) см.
Т.к. площадь квадрата находят по формуле S = а², где а - сторона квадрата, о площадь данного квадрата равна (х²) см².
А т.к площадь прямоугольника находят по формуле S = a · b, где a и b - длина и ширина прямоугольника, то площадь данного прямоугольника будет равна S = 3х · (х - 5) = 3х² - 15х (см²).
Т.к. площадь квадрата на 50 см² меньше площади прямоугольника, то составим и решим уравнение:
3x² - 15х = x² + 50,
3x² - x² - 15x - 50 = 0,
2x² - 15x - 50 = 0,
D = (-15)² - 4 · 2 · (-50) = 225 + 400 = 625 ; √625 = 25,
x₁ = (15 + 25)/(2 · 2) = 40/4 = 10,
x₂ = (15 - 25)/(2 · 2) = -10·/4 = -2,5 - не подходит по условию задачи.
Значит, сторона квадрата равна 10 см.
ответ: 10 см.