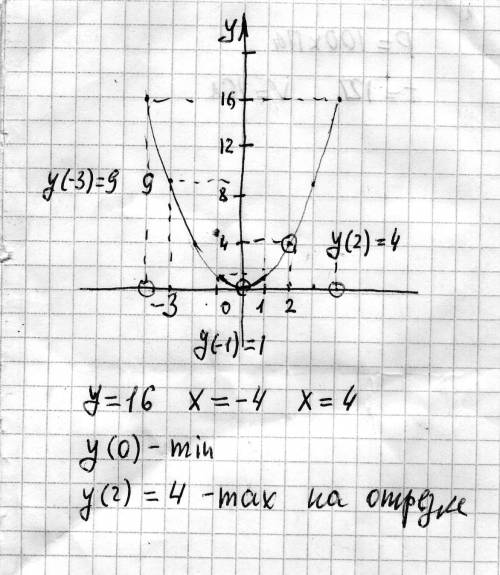
Смотри график во вложении!
Это квадратичная парабола, ветви вверх
А)
y(-3) = (-3)^2 = 9
y(-1) = (-1)^2 = 1
y(2) = 2^2 =4
Б)
x^2=16
x=±4
В)
Из графика видно, что на отрезке [-1;2] наим. значение достигается при x=0
ymin=y(0)=0
наиб. значение при x=2 ⇒ymax=y(2)=4
кубическая функция может иметь только локальный минимум. Потому что при х ->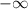 
она уходит в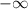
точки минимума и максимума соответствуют нулям производной
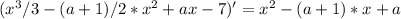
сумма степеней равна нулю, значит один корень = 1, второй = a
локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)
значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7 
при а>1 локальный минимум f(x=a) = a^3/3-(a+1)/2*a^2+a^2 - 7 = (1/3 - 1/2) a^3 + (-1/2+1) a^2 - 7 = - a^3 / 6 + a^2 / 2 - 7
при a = 1 имеем точку перегиба и никакого минимума
решение в приложении.....................................