раскрываешь скобки просто
x^2-2x-11x+22-8x+6x^2 = 7x^2-21x+22
Введем обозначения:
k - площадь, занятая кукурузой
a - площадь, занятая овсом
p - площадь, занятая пшеном
x - свободная площадь
S - площадь всего поля
По условию, если свободную часть поля полностью засадить пшеном, то пшено будет занимать половину всего поля. Но тогда и кукуруза вместе с овсом будут тоже занимать половину поля. Получаем равенства:
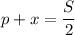(1)
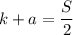(2)
По условию, если свободную часть поля поровну поделить между овсом и кукурузой, то овёс будет занимать половину всего поля. Но тогда и кукуруза вместе с пшеном будет занимать половину поля. Получаем равенства:
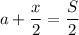(3)
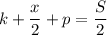(4)
Составим выражение, которое будет отвечать на вопрос задачи. Если свободную часть поля отдать под кукурузу, то она будет занимать площадь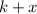 
, хотя до этого она занимала площадь 
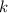. Соответственно, площадь увеличилась в 
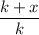раз.
Значит, нужно найти связь между k и x.
Заметим, что правые части уравнений (1)-(4) равны. Удобно приравнять левые части (2) и (3) уравнения, так как в них кроме переменных k и x встречается только переменная a, причем в одинаковом выражении, которое впоследствии взаимно уничтожится:
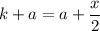
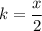
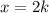
Подставим в искомое выражение:
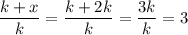
ответ: в 3 раза
4) (12х^5/25) × (15/8х^2) = (3х^3/5) × (3/2) = 9х^3/10 (сокращаем 12х^5 и 8х^2, сокращаем 25 и 15)
6) иксы сокращаем и умножаем = 3/4
8) (16х^5/35) × (5/8х^3) = 2х^2/7 (сокращаем 16х^5 и 8х^3, сокращаем 35 и 5)
10) (9/2а) × (5а/3) = 3/2 × 5 = 15/2 = 7,5 (сокращаем 9 и 3, сокращаем 5а и 2а)
12) (3/4а^3) × (16а^2/9) = (1/а) × (4/3) = 4/3а (сокращаем 3 и 9, сокращаем 16а^2 и 4а^2)
14) (15/3аб) × (12б^3/3) = (5/а) × 4б^2 = 20б^2/а (сокращаем 15 и 3, сокращаем 12б^3 и 3б)
15) (18/с^4) × (с^3/24) = (3/с) × (1/4) = 3/4с (сокращаем 18 и 24, сокращаем с^3 и с^3)
x^2-11x-2x+22-8x+6x^2=7x^2-21x+22надеюсь,что все правильно сосчитала)