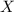 , все цифры их
, все цифры их 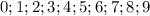 , так как по свойству, число делится на 9 тогда и ,только тогда , когда сумма цифр делиться на 9 , очевидно сумма равна 45 и она делится . Надо найти порядок этих цифр составляющие число
, так как по свойству, число делится на 9 тогда и ,только тогда , когда сумма цифр делиться на 9 , очевидно сумма равна 45 и она делится . Надо найти порядок этих цифр составляющие число 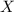
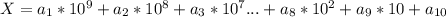
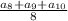 должно выполняться !
должно выполняться !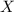 было наименьшим подходит 768
было наименьшим подходит 768 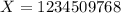
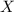 , все цифры их
, все цифры их 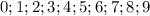 , так как по свойству, число делится на 9 тогда и ,только тогда , когда сумма цифр делиться на 9 , очевидно сумма равна 45 и она делится . Надо найти порядок этих цифр составляющие число
, так как по свойству, число делится на 9 тогда и ,только тогда , когда сумма цифр делиться на 9 , очевидно сумма равна 45 и она делится . Надо найти порядок этих цифр составляющие число 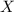
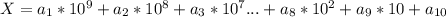
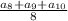 должно выполняться !
должно выполняться !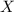 было наименьшим подходит 768
было наименьшим подходит 768 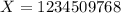
1)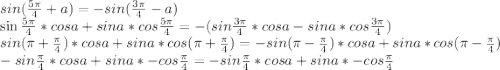
Доказано.
Доказано.