
Объяснение:
С графика читаем любые две точки на прямой:
A(0;0) , B(-2;3)
f(0)=0
f(2)=-3
общая формула для линейной функции:
: f(x)=kx+b
воспользуемся системой линейных уравнений, в которую подставим координаты точек A и B
{k*0+b=0 {b=0 {b=0 {b=0 == > {b=0
{k*2+b=-3 == > {2k+0=-3 == > {-2k=-3 == > {k=-3/2 == > {k=-1,5x
Итак, формула для поиска линейной функции: y = -3 / 2 x
Чтобы проверить, я вляется ли данная пара чисел решением системы уравнений, нужно в вместо х и у в систему подставить эти значения и вычислить. Если получатся верные равенства - это значит, что пара чисел - решение системы.
Поэтому:
данная система: х + у = -5, х² - у² = 13.
1) (2; -7) - подставляем: 2 + (-7) = -5,
2² - (-7)² = 4 - 49 = -45 ≠ 13, значит, не является;
2) (-5; 0) - подставляем: -5 + 0 = -5 и (-5)² - 0² ≠ 13, значит, не является;
3) (-3,8; -1,2) - подставляем: -3,8 + (-1,2) = -5,
(-3,8)² - (-1,2)² = 14,44 - 1,44 = 13, значит, является;
4) (-3,8; -1,8) - подставляем: -3,8 + (-1,8) = -5,6 ≠ -5, значит, не является.
ответ: 3) (-3,8; -1,2).
3) (-3,8; -1,2)
Объяснение:
Известно, что если пара чисел является решением системы уравнений, то эта пара удовлетворяет каждое уравнение системы. Поэтому, достаточно подставить вместо х и у в уравнения системы значения чисел этой пары и вычислить. Если для какого-то уравнения равенство не выполняется, то процесс проверки останавливаем и объявляем вердикт "не является решением", а если для всех уравнений получаются верные равенства, то пара чисел является решением системы и объявляем вердикт "является решением".
Дана система уравнений:
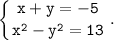
1) (2; -7) - подставляем:
1-уравнение: 2 + (-7) = -5 - выполнено,
2-уравнение: 2² - (-7)² = 4 - 49 = -45 ≠ 13 - не является решением;
2) (-5; 0) - подставляем:
1-уравнение: -5 + 0 = -5 - выполнено,
2-уравнение: (-5)² - 0² = 25 ≠ 13 - не является решением;
3) (-3,8; -1,2) - подставляем:
1-уравнение: -3,8 + (-1,2) = -5 - выполнено,
2-уравнение: (-3,8)² - (-1,2)² = 14,44 - 1,44 = 13 - является решением;
4) (-3,8; -1,8) - подставляем:
1-уравнение: -3,8 + (-1,8) = -5,6 ≠ -5 - не является решением.
y=0 x=0
Объяснение:
томущо за основними формулами шрафіка