Наименьшее общее кратное двух чисел - это произведение простых множителей, взятых в наибольшем количестве от одного из этих двух чисел.
НОК (a, b) = 222 = 2 · 3 · 37
Возможные варианты чисел a,b по убыванию: 222, 111, 74, 37, 6, 3, 2, 1.
Под условие a>b подходят следующие пары :
a = 222 =2·3·37 - так как 222 содержит все простые множители НОК, то число b может принимать любое значение из возможных вариантов.
a = 222; b = 111; b = 74; b = 37; b = 6; b = 3; b = 2; b = 1
a = 111 = 3·37 - не хватает множителя 2, поэтому в пару можно ставить только чётные числа из возможных вариантов.
a = 111; b = 74; b = 6; b = 2
a = 74 = 2·37 - не хватает множителя 3, поэтому в пару можно ставить только числа, кратные трём.
a = 74; b = 6; b = 3
a = 37 - не хватает множителей 2 и 3, поэтому остается один вариант
a = 37; b = 6
Всего получилось 13 пар чисел (a,b), удовлетворяющих условию :
(222; 111); (222; 74); (222; 37); (222; 6); (222; 3); (222; 2); (222; 1)
(111; 74); (111; 6); (111; 2); (74; 6); (74; 3); (37; 6)
5 чёрных шариков
Объяснение:
формула вероятности р = Ν пол. / Ν всех
Ν пол. - количество положительных исходов
Ν всех - количество всех исходов
Положительные исходы: чёрные шарики - Х шт
Не положительные исходы: жёлтые шарики - 15 шт
Все исходы: чёрные + жёлтые= Х+15 шт
Вероятность р = Ν пол. / Ν всех, то есть 1/4 = Х / Х+15
решим уравнение: 1/4 = Х / (Х+15)
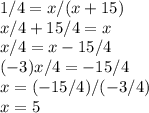 - чёрных шариков.
- чёрных шариков.
ВТОРОЙ ВАРИАНТ РЕШЕНИЯ.
Можно решить проще, логическим решением.
ЧШ - чёрные шарики
ЖШ - жёлтые шарики
ВШ - все шарики вместе
Вероятность р = Ν пол. / Ν всех, то есть р = ЧШ / ВШ
Жёлтых ш. - 15; чёрных ш. - Х; всех ш. - 15+х
Если вероятность р = 1/4, это отношение чёрных к общему количеству: ЧШ / ВШ = 1/4. То тогда отношение ЖШ / ВШ = 3/4
И раз 3/4 - это 15 шариков (жёлтых), то соответственно 1/4 - это 5 шариков (чёрных)
P=C₈³ p³q⁵= 56(0,3)³(1-0,3)⁵=56 * 0,027 * 0,16807≈0,2541
Это формула Бернулли