Если уравнение имеет целые корни, то они являются делителями свободного члена. Методом пристального взгляда замечаем, что x = -1 обращает уравнение в верное числовое равенство. А это значит, что в разложении на линейные множители точно будет множитель (x + 1).
*тут должно было быть деление в столбик, но я не знаю, как его вставить сюда*
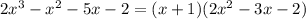
А дальше произведение равно нулю тогда, когда один из множителей равен нулю, а остальные существуют.
Откуда находим еще два решения: x = 2 и x = -0.5
ответ: x = -1, -0.5, 2
3x + 2y = 8;
2x + 6y = 10,
применим метод подстановки. И начнем мы с того, что второе уравнение разделим на 2 и получим:
3x + 2y = 8;
x + 3y = 5.
Выражаем из второго уравнения переменную x:
x = 5 - 3y;
3x + 2y = 8.
Подставляем вместо x выражение из первого уравнения.
x = 5 - 3y;
3(5 - 3y) + 2y = 8.
Решаем первое уравнение системы:
3 * 5 - 3 * 3y + 2y = 8;
15 - 9y + 2y = 8;
-9y + 2y = 8 - 15;
-7y = -7;
y = 1.
Система уравнений:
x = 5 - 3 * 1 = 5 - 3 = 2;
y = 1.