Четность функции allcalc.ru
parity f(x)=
x^3/(4(2-x)^2 )
Вычислить
Основные функции
\left(a=\operatorname{const} \right)
x^{a}: x^a
модуль x: abs(x)
\sqrt{x}: Sqrt[x]
\sqrt[n]{x}: x^(1/n)
a^{x}: a^x
\log_{a}x: Log[a, x]
\ln x: Log[x]
\cos x: cos[x] или Cos[x]
\sin x: sin[x] или Sin[x]
\operatorname{tg}x: tan[x] или Tan[x]
\operatorname{ctg}x: cot[x] или Cot[x]
\sec x: sec[x] или Sec[x]
\operatorname{cosec} x: csc[x] или Csc[x]
\arccos x: ArcCos[x]
\arcsin x: ArcSin[x]
\operatorname{arctg} x: ArcTan[x]
\operatorname{arcctg} x: ArcCot[x]
\operatorname{arcsec} x: ArcSec[x]
\operatorname{arccosec} x: ArcCsc[x]
\operatorname{ch} x: cosh[x] или Cosh[x]
\operatorname{sh} x: sinh[x] или Sinh[x]
\operatorname{th} x: tanh[x] или Tanh[x]
\operatorname{cth} x: coth[x] или Coth[x]
\operatorname{sech} x: sech[x] или Sech[x]
\operatorname{cosech} x: csch[x] или Csch[е]
\operatorname{areach} x: ArcCosh[x]
\operatorname{areash} x: ArcSinh[x]
\operatorname{areath} x: ArcTanh[x]
\operatorname{areacth} x: ArcCoth[x]
\operatorname{areasech} x: ArcSech[x]
\operatorname{areacosech} x: ArcCsch[x]
[19.67] =19: integral part of (19.67) - выделяет целую часть числа (integerPart)
Объяснение:
ну смотри.
Возьмём в пример это:
(а+4)(6+а)
Мы должны умножать дугой: а×6=6а, а×а=а², 4×6=24, 4×а=4а.
Я прикреплю фото, чтобы было понятнее.
ответом будет являться: 6а+а²+24+4а.
Но ответ не окончательный, убираем подобные: 6а и 4а.
ответ: 10а+а²+24.
Выражение в виде произведения многочленов.
Пример:
а(m-3)+b(m-3)
В данном случае общим множителем является многочлен m-3. Поэтому выносим его в начало, а множители за скобками складываем и умножаем;
(m-3)(a+b)
Метод группировки.
Метод группировки - это разложение многочлена на множители, объединив в группы его члены.
Пример:
2ас+2bc+5am+5bm
Сгруппировать члены этого многочлена нужно так, чтобы слагаемые в каждой группе имели общий множитель.
2ас+2bc+5am+5bm=(2ac+2bc)+(5am+5bm)=
=2c(a+b)+5m(a+b)=(a+b)(2c+5m).
Ничего сложного нет, нужно это только понять.)
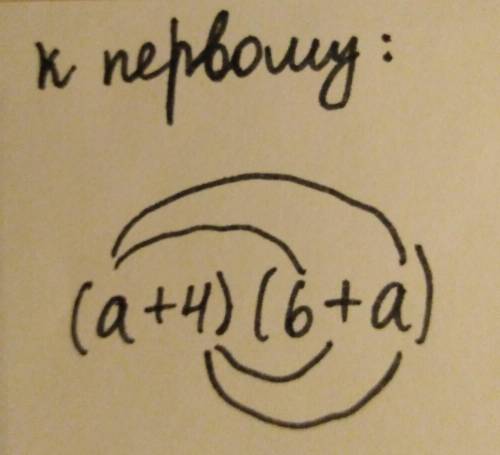
x³-y³=(x-y)(x²+xy+y²).