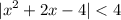
раскроем модуль:
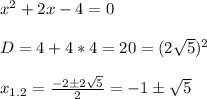
_+___ -1 -√5 ___-___ -1+√5__+__
x²+2x-4 -x²-2x+4 x²+2x-4
1) теперь рассмотрим решение неравенства на промежутках
(-∞; -1-√5] ∪ [-1+√5; +∞)
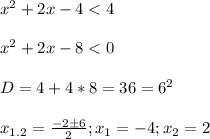
_\\\\\\ -4 _\\\\\ -1-√5_____ -1+√5_\\\\\\_ 2__\\\\\__
////////////////////////////////////////////////
пересечением решений будут промежутки
(-4; -1-√5] ∪ [-1+√5;2)
2) теперь рассмотрим решение неравенства на промежутках
(-1-√5;-1+√5)
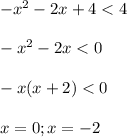
_____ -1-√5_ \\\\\\_ -2_\\\\\\_ 0_\\\\\_-1+√5_____
//////////////////////////// /////////////////////
пересечением решений будут промежутки (-1-√5;-2) ∪ (0; -1+√5)
И Тогда общим ответом будет
(-4; -2) ∪ (0;2)
Две линейные функции вида y = kx + b могут, или быть параллельными друг другу, или пересекаться в одной точке.
Графиком линейной функции является прямая линия. Коэффициент k является угловым коэффициентом или, углом наклона прямой к положительному направлению оси 0Х.
Если k>0, то угол будет острым, т.е. прямая наклонена вправо от оси 0У.
При k < 0 прямая будет иметь тупой угол с осью 0Х, т.е. наклонена влево от оси 0У.
Если у двух линейных функций коэффициэнты k равны одному и тому же числу, то эти прямые параллельны относительно друг друга.
1) у=2х-10 и у=2х+9 - k=2 и k=2, 2=2, значит графики этих функций параллельны.
Коэффициент b определяет длину отрезка который пересекает прямая по оси 0У от начала координат (0;0) - точку, в которой график пересекает ось 0У.
Взаимное расположение прямых у=2х-10 и у=2х+9 можно посмотреть во вложении.
2) у=-3х+9 и у=-3х+9
k=-3; b=9 k=-3; b=9 => -3=-3; 9=9 если коэффициенты k и b обеих функций одинаковые, то графики таких функций совпадают. По сути, это один и тот же график.
3) у=-5х-6 и у=-5х; -5=-5 - графики параллельны.
4) у=1.5+4х и у=-4х+3
Нужно переписать 1-е уравнение в принятом виде y = kx + b:
у=4х+1.5 и у=-4х+3, 4 ≠ -4, значит прямые пересекаются.
5) у=7+2.3х и у=3.2х-1
у=2.3х+7 и у=3.2х-1; 2.3≠2.3, значит прямые пересекаются.
6) у=10х и у=1-10х
у=10х и у=-10х+1; 10≠-10 - графики пересекаются
Объяснение: