/////////////////////////////////
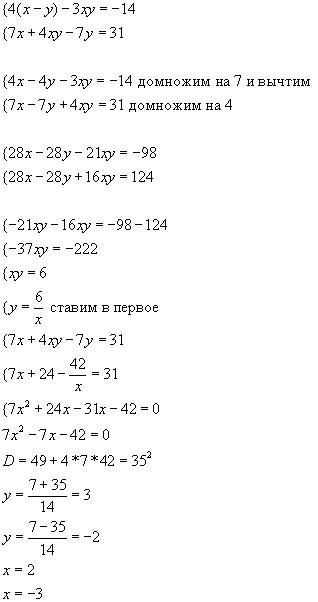
Пусть десятикопеечных монет у Ивана было "х" шт.
Всего монет было 25 шт., значит пятикопеечных у Ивана было "25-х" шт.
Зная, что их общая сумма денег равнялась 1 руб. 50 коп., составим уравнение:
(25-х) * 5 + 10х = 150;
125 - 5х + 10х = 150;
5х = 150 - 125;
5х = 125;
х = 125 : 5;
х = 5 (шт.) десятикопеечных монет было.
Всего было 25 монет, значит остальные пятикопеечные и их было:
25 - 5 = 20 (шт.) пятикопеечных монет было.
Объяснение:
Проверка.
20 * 5 + 5 * 10 = 150;
100 + 50 = 150;
150 = 150.
Чтобы выяснить, является ли число x = 5 корнем уравнения x^2 - 2x - 5 = 0 можно действовать двумя решить уравнение через дискриминант; 2) подставить данный корень вместо х в исходное уравнение и выполнив действия сделать вывод о полученном равенстве.
Итак, решать задачу будем вторым
Подставляем x = 5 в уравнение: x^2 - 2x - 5 = 0;
5^2 - 2 * 5 - 5 = 0;
25 - 10 - 5 = 0;
25 - 15 = 0;
10 = 0;
В результате мы получили неверное равенство. Делаем вывод, что х = 5 не является корнем уравнения.
ответ: не является корнем уравнения.
Объяснение:
4(x-y)-3xy=-14
7(x-y)+4xy=31
x-y=t
xy=s
4t-3s=-14 х4 16t-12s=-56
7t+4s=31 х3 21t+12s=93
37t=37
7+4s=31 4s=24 s=6
x-y=1
xy=6
x=2 y=3
x=-2 y=-3