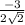
1)Решение системы уравнений х₁= -1 х₂=1
у₁=0,5 у₂=8
2)Решение системы уравнений х=4; у₁= -1; у₂=1.
Объяснение:
Решить систему уравнений:
1)(5х+3)²=8у
(3х+5)²=8у
Так как правые части равны, приравниваем и левые:
(5х+3)²=(3х+5)²
Раскрыть скобки:
25х²+30х+9=9х²+30х+25
Перенесём всё в левую часть, приравняем к нулю:
25х²+30х+9-9х²-30х-25=0
Приведём подобные члены:
16х²-16=0
Решим уравнение, вычислим значение х:
16х²=16
х²=1
х₁,₂=±√1
х₁= -1
х₂=1
Вычислим значение у:
8у₁=25х²+30х+9 х₁= -1
8у₁=25*(-1)²+30*(-1)+9
8у₁=25-30+9
8у₁=4
у₁=4/8
у₁=0,5
8у₂=25х²+30х+9 х₂= 1
8у₂=25*1²+30*1+9
8у₂=25+30+9
8у₂=64
у₂=64/8
у₂=8
Решение системы уравнений х₁= -1 х₂=1
у₁=0,5 у₂=8
2)3х²+2у²=50
12х²+8у²=50х
Упростить уравнения, первое разделить на 2, второе на 8:
1,5х²+у²=25
1,5х²+у²=6,25х
Умножить первое уравнение на -1, решить систему методом сложения:
-1,5х²-у²= -25
-1,5х²-у²+1,5х²+у²= -25+6,25х
0= -25+6,25х
-6,25х= -25
х= -25/-6,25
х=4
Теперь подставить значение х в любое из двух уравнений системы и вычислить у:
1,5х²+у²=25
у²=25-1,5х²
у²=25-1,5*4²
у²=25-24
у²=1
у₁,₂=±√1
у₁= -1
у₂=1
Решение системы уравнений х=4; у₁= -1; у₂=1.
В решении.
Объяснение:
Формула координат вершины параболы:
х₀ = -b/2a
y₀ = (4ac - b²)/4a, или просто подставить вычисленное значение х₀ в уравнение функции и вычислить значение у₀.
1) у = х² -10х + 20
х₀ = -b/2a
х₀ = 10/2
х₀ = 5;
у₀ = 5² - 10*5 + 20 = 25 - 50 + 20 = -5.
Координаты вершины параболы (5; -5). Ветви вверх.
2) y = -x² + 3x - 4
х₀ = -b/2a
х₀ = -3/-2
х₀ = 1,5;
у₀ = -(1,5)² + 3*1,5 - 4 = -2,25 + 4,5 - 4 = -1,75.
Координаты вершины параболы (1,5; -1,75). Ветви вниз.
3) у= -х² + 6х - 7
х₀ = -b/2a
х₀ = -6/-2
х₀ = 3;
у₀ = -(3)² + 6*3 - 7 = -9 + 18 - 7 = 2.
Координаты вершины параболы (3; 2). Ветви вниз.
4) у = 3х² - 6х + 1
х₀ = -b/2a
х₀ = 6/6
х₀ = 1;
у₀ = 3*1² - 6*1 + 1 = 3 - 6 + 1 = -2.
Координаты вершины параболы (1; -2). Ветви вверх.
5) у = -0,2х² + 4х
х₀ = -b/2a
х₀ = -4/-0,4
х₀ = 10;
у₀ = -0,2*10² + 4*10 = -0,2*100 + 40 = -20 + 40 = 20.
Координаты вершины параболы (10; 20). Ветви вниз.