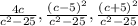1. 8х^2 = 32 | 8 // Поділили обидві частини рівняння на 8.
х^2 = 1
х = +-1 // Які числа у квадраті дають 1? 1 і -1.
2. 3х^2 - 48х = 0 // тут винесемо спільний множник за дужки.
3х × (х - 16) = 0 // Оце воно. Коли добуток дорівнює нулю, то або один, або два множники дорівнюють нулю.
2.1. 3х = 0
х = 0
2.2. х - 16 = 0
х = 16
3. 6х^2 + 5х - 4 = 0 // Тут вже дискримінантом.
D = 25 - 4 × (-4) × 6 = 25 + 24 × 6 = 25 + 144 = 169
х1 = -5 - 13 / 12 // Я делю на 12 не только -13, а всё выражение // = -18 / 12 = -3/2
х2 = -5 + 13 / 12 = 8/12 = 2/3
Если что-то не правильно, то пишите - всё исправим.
d = 8/5
Объяснение:
5x^2-6x+d=0
Пусть
x_1 = 2x_2, где
x_1 - первый корень квадратного уравнения
x_2 - второй корень квадратного уравнения,
тогда по теореме Виета (дла случая а≠1) запишем систему:
(x_2)*(2x_2)= d/5;
x_2+2x_2= 6/5;
решаем:
2*(x_2)^2=d/5;
3x_2=6/5;
далее:
2(x_2)^2=d/5;
x_2=6/(5*3) = 2/5;
подставим в первое уравнение
2*((2/5)^2)=d/5;
d/5= 2*4/25=8/25;
d/5=8/25;
d=40/25=8/5
Проверка:
5x^2-6x+8/5=0
D=6^2-4*5*8/5=36-32=4;
x_12=1/10*(6±√(4));
x_1= 8/10; x_2=4/10
x_1/x_2=(8/10)/(4/10)=2 как в условии!
x_1*x_2=8/10*4/10=32/100=8/25=d/5 - правильно
x_1+x_2=4/10+8/10=12/10=6/5=-(-6)/5 - верно!
Объяснение:
1,59 в)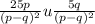
1.59 г)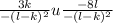
1.64 в)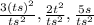
1.65 в)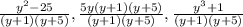
1.65 г)