≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =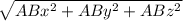 
|AB| =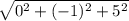 
|AB| =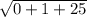 
|AB| =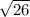 
|CD| =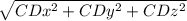 
|CD| =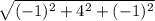 
|CD| =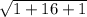 
|CD| =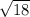 
|CD| = 3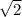
Найдем косинус угла между векторами:
cos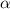 
= 
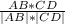
cos =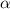 
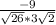
cos =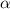 
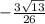
cos 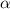= ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°
ответ: Уравнение эллипса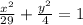 
; оси симметрии данного эллипса являются осями координат(или ось Ох и Оу); ε =5/√(29)
Объяснение:
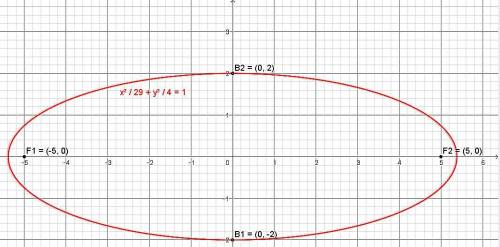
Дан эллипс: F₁ =(-5;0); F₂ =(5;0) и B₁=(0;-2); B₂=(0;2). Напишите уравнение эллипса, найти оси и эксцентриситет
фокусное расстояние эллипса с = 5 (от точки F до точки О)
малая полуось b = 2
большая полуось а находится из соотношения
а² = b² + c²
a² = 2² + 5² = 4 + 25 = 29
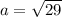
уравнение эллипса:
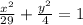
- каноническое уравнение эллипса
Оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии.
Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .
ε = с/ a = 5/√(29)
1) 0.25 ^ (3-2X) < _ 16
0.25 = 25\100 = 1\4 = 2^ (-2)
16 = 2 ^4
(2 ^( -2))^(3-2X) < _ 2 ^ 4
-2 * (3 - 2X ) < _ 4
- 6 + 4X < _ 4
4X < _ 10
X < _ 2.5
ответ от минуса бесконечность до 2.5 (2.5 входит)
2) 2 ^ X + 2 ^ (X-1) - 2 ^ (X-3) = 44
2 ^X + 2 ^X * 1\2 - 2 ^ X * 1\8 = 44
2^X *( 1 + 1\2 - 1\8) = 44
2^ X = 44 : 11\8
2^X = 32
2^X = 2^ 5
X = 5
ответ: Х = 5
3) 9 ^ (7-X) < _ 27
9 ^ 7 : 9 ^X < _ 27
9^X < _ 9 ^ 7 : 27
3^2X < _ 3 ^ (14 - 3)
3 ^ 2X < _ 3 ^ 11
2X < _ 11
X < _ 5.5
ответ : от минуса бесконечность до 5.5 (число 5.5 входит)