Объяснение:
нам для решения нужны два свойства. логарифм числа а по основанию а равен единице, логарифм числа а в степени к по любому основанию равен к умножить на логарифм числа а по любому основанию. Как мы знаем если домножить число на единицу, оно не изменится, тогда
домножим правую часть первого уравнения на логарифм числа 6 по основанию 6, а второе уравнение на логарифм числа 18 по основанию 18, тогда
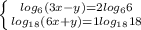 . уберем в 1-ом уравнении двойку в степень подлогарифмического, получим логарифм числа 36 по основанию 6. Теперь при равенстве логарифмов по одному основанию левых и правых частей, перейдем к равенству, подлогарифмических левых и правых частей, но теперь нужно учесть, что значения переменной х и у должны удовлетвореть ОДЗ: а именно, подлогарифмические выражение должны быть больше нуля, т.е. 3x-y>0 6x+y>0.
. уберем в 1-ом уравнении двойку в степень подлогарифмического, получим логарифм числа 36 по основанию 6. Теперь при равенстве логарифмов по одному основанию левых и правых частей, перейдем к равенству, подлогарифмических левых и правых частей, но теперь нужно учесть, что значения переменной х и у должны удовлетвореть ОДЗ: а именно, подлогарифмические выражение должны быть больше нуля, т.е. 3x-y>0 6x+y>0.
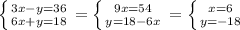 Проверим корни на принадлежность ОДХ
Проверим корни на принадлежность ОДХ
3*6-(-18) больше нуля.
6*6-18 так же больше нуля, значит эта пара чисел и есть решение системы.
2)
домножим 4 на логарифм 3 по основанию 3, и отправим 4 в степень, тогда
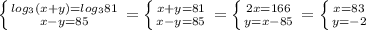 . Проверим ОДЗ
. Проверим ОДЗ
х+у должно быть болье нуля и это верно. значит пара чисел 83 минус 2 - решение
3) Тут нужно вспомнить еще одно свойство, что сумма логарифмов по одному основанию равна логарифму произведения по этому основанию, тогда
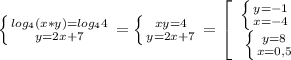 Т.к. по ОДЗ и икс и игрик должны быть больше нуля, то первая пара нас не устраивает, а значит ответ пара чисел 1/2 и 8
Т.к. по ОДЗ и икс и игрик должны быть больше нуля, то первая пара нас не устраивает, а значит ответ пара чисел 1/2 и 8
4)
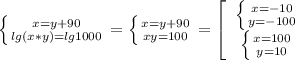 , икс и игрик должны быть положительны, поэтому только вторая пара 100 и 10 нас устраивает. (если что lg это десятичный логарифм, т.е. логарифм по основанию 10)
, икс и игрик должны быть положительны, поэтому только вторая пара 100 и 10 нас устраивает. (если что lg это десятичный логарифм, т.е. логарифм по основанию 10)
-1/3
Объяснение:
если все слагаемые поделить на высшую степень переменной, то в знаменателе все равно окажется ноль, что недопустимо. есть правило Лопиталя, по которому ты находишь производную числителя и знаменателя, пока у тебя в знаменателе будет нечто, что не равно нулю. находим по Лопиталю. Можешь это сделать сама получается ты применяешь ее 1 раз, подставляешь, снова знаменатель равен нулю, еще раз применяешь правило Лопиталя. от тех функции, которые у тебя получились. Подставляешь x0 в данную дробь и получаешь -1/3
D(y) = R (а что еще можно ждать от полинома?)
Найдем первые 2 производные:
y'=2*3x^2-3*2x-12*1-13=6x^2-6x-12
y''=12x-6
(пользуемся линейностью (c1*f+c2*g)'=c1*f'+c2*g' и формулой (x^r)'=r*x^(r-1))
Функция возрастает там, где ее производная неотрицательна. Решаем неравенство y'>=0:
6x^2-6x-12>=0
x^2-x-2>=0
(x-2)(x+1)>=0
x in (-infty,-1] U [2, +infty)
При таких х функция возрастает, тогда, очевидно, функция убывает на [-1, 2].
В точке x=-1 производная меняет знак с плюса на минус, поэтому это точка максимума. В точке x=2 всё наоборот, точка минимума.
Функция выпукла, если ее вторая производная неотрицательна.
y''>=0
12x-6>=0
2x>=1
x>=1/2
При x>=1/2 функция выпукла, при x<=1/2 функция вогнута. x=1/2 - точка перегиба.