При имеющихся исходных данным возможно 2 ответа:
1) b₁ = 6; q = 1/4;
1) b₁ = -6; q = -1/4;
Объяснение:
Член геометрической прогрессии с номером n вычисляется по формуле
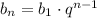
b₄ - b₂ = b₁ · q³ - b₁· q = b₁q(q² - 1)
b₆ - b₄ = b₁ · q⁵ - b₁· q³ = b₁q³(q² - 1)
По условию
b₁q(q² - 1) = -45/32 (1)
b₁q³(q² - 1) = -45/512 (2)
Преобразуем выражение (2)
b₁q³(q² - 1) = b₁q(q² - 1) · q²
В численном виде это можно записать как
-45/512 = -45/32 · q²
Откуда
q² = -45/512 : (-45/32)
q² = 1/16
q = ±1/4
Подставим q = 1/4 в выражение (1)
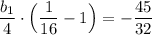
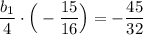
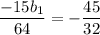
0.5b₁ = 3
b₁ = 6
Подставим q = -1/4 в выражение (1)
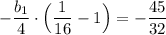
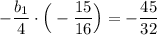

0.5b₁ = -3
b₁ = -6
Проверка:
1) b₁ = 6; q = 1/4
b₂ = 6 · 1/4 = 3/2
b₄ = 6 · 1/64 = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = 6 · 1/1024 = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
2) b₁ = -6; q = -1/4
b₂ = -6 · (-1/4) = 3/2
b₄ = -6 · (-1/64) = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = -6 · (-1/1024) = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
z1+z2=1+j+(-2-3j)=-1-2j
z1*z2+(1+j)(-2-3j)=-2-3j-2j-3j^2=-2-5j-3j^2
z1/z2=(1+j)/(-2-3j)=-(1+j)/(2+3j)
z1-z2=1+j-(-2-3j)=1+j+2+3j=3+4j
вроде так,если правильно поняла задание