а) При сравнении десятичных дробей в первую очередь нужно сравнивать целые части (они расположены слева от запятой). Так как целые части равны, то сравниваем дробные части
0.382 < 3*2 ⇔ 0.382 < 0.392 ⇒ потому что 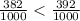
Следовательно, 5.382 < 5.392
б) Аналогично, целые части равны, тогда сравниваем дробные части
0.* < 0.2 ⇔ 0.1 < 0.2 так как 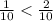
Следовательно, 31.1 < 31.2
в) У первого числа символов после запятой не совпадает со вторым числом, тогда к дроби наименьшим количеством символов приписываем нули и сравним получившиеся числа дробных частей
0.10 > 0.*1 ⇔ 0.10 > 0.01 так как 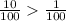
Следовательно, 7.1 > 7.01
г) Аналогично с примера в), рассуждения такие же:
0.010 < 0.*08 ⇔ 0.010 < 0.108 потому что 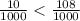
Следовательно, 7.01 < 7.108
х = -204
Объяснение:
Дано:
функция y=3x+3
у = - 609
Найти:
х
Подставим в уравнение функции вместо у его значение (- 609) и решим уравнение относительно х:
- 609 =3х+3
- 609 - 3 = 3х
3х= -612
х = (-612) : 3
х = -204
х = -204