пара чисел (1;-6) для уравнения p^2*x+p*y+8=0
p^2 - 6p + 8 = 0
D = 36 - 4*8 = 36 - 32 = 4 = 2^2
p1 = (6-2)/2 = 2 p2 = (6+2)/2 = 4
p^2-6p+8=0
р*р - 4р - 2р + 2*4 = 0 (разложим на множители)
сгрупируем по парам - первые два(тут можно за скобки вынести "р")
и вторые сгрупируем - тут вынесим за скобки "-2" )
р * ( р - 4) - 2 (р - 4) = 0
теперь опять как бы вынесим за скобки (р-4)
(р-4) (р-2) = 0
р - 4 = 0 и р - 2 = 0
р = 4 р = 2
данная пара чисел (1;-6) будет являться решением уравнения p^2*x+p*y+8=0 при р = 2 или р = 4
у=2(х-2)*-1
у=(2х-4)*-1
у=-2х+4
f(x)=-2x+4 - линейная функция, график - прямая
Область определения D(f) x∈R (множество всех действительных чисел)
Множество значений E(f) y∈R я
Нет максимума и минимума, непериодическая (непрерывна), ни четная, ни нечетная.
k=-2 => k<0 - функция убывающая, график образует тупой угол с положительным направлением оси 0Х.
График строится по 2-м точкам.
Можно найти точки пересечения графика с осями координат и построить график по ним.
Пересечение с осью 0Х: х=0 => y=-2*0+4=4 (0;4)
Пересечение с осью 0У: y=0 => х=-4/-2=2 (2;0)
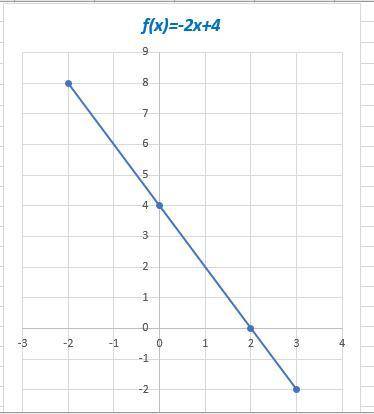
Смотри решение на фото