общая формула для нахождения касательной к графику функции имеет вид
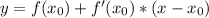
точка касания нам известна 
1. найдем значение функции в точке касания
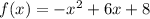
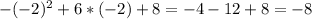
2. найдем производную функции
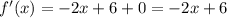
3. найдем значение производной в точке касания
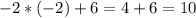
4. подставим в формулу полученные результаты
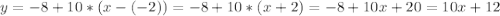
Объяснение:
1) Площадка перед гаражом занимает 4*14 = 56 плиток.
Дорожки занимают 29 плиток.
Всего получается 56 + 29 = 85 плиток.
Если плитки продаются пачками по 20 штук, то нужно 85 = 4*20 + 5, то есть 5 пачек.
2) Разберемся, что где находится.
7 - колодец, 8 - гараж, 6 - дом, 1 - теплица, 2 - огород, 5 - пруд, 4 - сарай, 3 - баня.
Сарай 4 имеет размеры 4*8 = 32 кв.м.
Баня имеет размеры 4*4 = 16 кв.м.
Суммарная площадь сарая и бани:
S = 32 + 16 = 48 кв.м.
3) Пройти от угла теплицы 1 до угла пруда 5 можно по гипотенузе прямоугольного треугольника, у которого один катет 2*3 = 6 м, а второй 2*4 = 8 м.
Длина пути:
L = √(6^2 + 8^2) = √(36 + 64) = √100 = 10 м.
4) Как мы знаем из п. 1, нужно 85 кв.м. плиток.
У 1 поставщика плитка будет стоить 85*200 = 17000 руб.
Доставка 1500 руб. и работа 1000 руб.
Всего 17000 + 1500 + 1000 = 19500 руб.
У 2 поставщика плитка будет стоить тоже 85*200 = 17000 руб.
Доставка 2000 руб. и работа бесплатно.
Всего 17000 + 2000 = 19000 руб.
У 3 поставщика плитка будет стоить 85*220 = 18700 руб.
Доставка бесплатно и работа 1700 руб.
Всего 18700 + 1700 = 20400 руб.
Самый выгодный - поставщик номер 2.
Обозначим длину прямоугольника как а, ширину прямоугольника как b, и диагональ как c.
Рассмотрим ΔABC: ∠B=90° ⇒ ΔABC - прямоугольный; a,b - катеты, c - гипотенуза
т. Пифагора гласит:
a² + b² = c²
a² + b² = 13²
a² + b² = 169
А площадь прямоугольника находится по формуле:
S = a * b
a * b = 60
Составим систему уравнений и решим методом подстановки.
Вводим новую переменную.
b² = t - новая переменная.
b² = t
b² = 25 или b² = 144
b₁ = 5; b₂=-5; b₃=12; b₄=-12
Т.к. сторона не может быть отрицательна, то -5 и -12 не подходят.
a * b = 60
a₁ * 5 = 60
a₁ = 12
a₂ * 12 = 60
a₂ = 5
⇒ Стороны прямоугольника равны 5 см и 12 см.
ответ: 5 см; 12 см
касательнaя ест просто производной в точке
потому решаем производную.
f ' (x) = (-x^2 )' + (6x)' + (8)' = (-2)x + 6 + 0 = 6 - 2x
f '(-2) = 6 - 2(-2) = 10
тут красиво видно почему то производную по иксе записываем тоже так
df(x) / dx значит: сколко изменилос функции до изменения икса
решене число 10 = df(x) / dx = tg ( угла касателной )
значит это А в уровнению прямой : y= Ax+B
оттуда знаем что наша касательная иммеет уровнение y = 10x +B
искана касателная имеет в точке такие значениe как дана функция
f(-2) = f ' (-2) = -(-2)^2 + 6(-2) + 8 = -4 - 12 + 8 = (-8)
вернуемся к касателно, решаем число B
y =10x + B ; y = -8 ; x= -2
-8 = 10(-2) + B
-8 = -20 + B
B = -8 +20 = 12
уровнение касательной :
y = 10 x +12
сделаем граф - во вложению