Задание:
Решите уравнение.
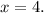
Объяснение:
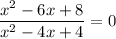
Дробь равна нулю, если числитель ему равен, а знаменатель — нет:
Так как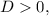 
то уравнение будет иметь два действительные корни, которые находятся по формуле:
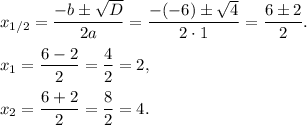
Но теперь надо проверить: подходят ли эти корни:
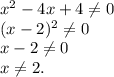
Теперь можем выяснить, что корень 
не подходит, так как не входит в ОДЗ.
Для точной проверки можно подставить корень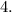 
Но это делать не обязательно:
Да, действительно корень 
является решением уравнения.
Также можно доказать, что корень 
не является решением:
Все правильно, так как на ноль делить нельзя.
Задание:
Решите уравнение.
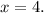
Объяснение:
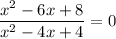
Дробь равна нулю, если числитель ему равен, а знаменатель — нет:
Так как 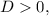то уравнение будет иметь два действительные корни, которые находятся по формуле:
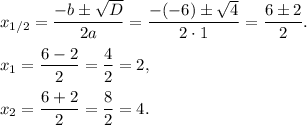
Но теперь надо проверить: подходят ли эти корни:
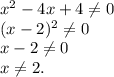
Теперь можем выяснить, что корень не подходит, так как не входит в ОДЗ.
Для точной проверки можно подставить корень 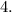Но это делать не обязательно:
Да, действительно корень является решением уравнения.
Также можно доказать, что корень не является решением:
Все правильно, так как на ноль делить нельзя.
1)ab(a^2-4b^2)=ab(a-2b)(a+2b)
2)7(a^2-2ab+b^2)=7(a-b)^2
3)(x^2+2x+1)-(y^2+6y+9)=(x+1)^2-(y+3)^2=(x+1-y-3)(x+1+y+3)=(x-y-2)(x+y+4)