Объяснение:
См. на фотографии.
Допустим, возможна такая раскраска, что не образует одноцветного треугольника. Исследуем это допущение.
Рассмотрим произвольный треугольник в любом из 6-угольников, образованный тремя вершинами (через одну) 6-угольника мозаики.
Очевидно, что из трех вершин такого треугольника две будут одинакового цвета.
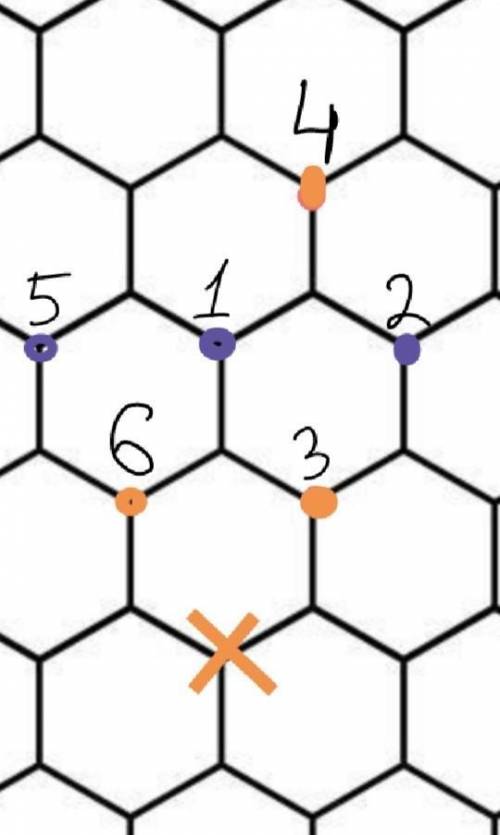
Пусть, это будет треугольник (123), а "одинаковый цвет" - черный. (здесь и далее см. рисунок)
Допустим, точки 1 и 2 - черного цвета. Тогда очевидно, что т.3 - белая, ибо иначе будет одноцветный треугольник (123). По той же причине, белая будет т.4 (треугольник (124) не может быть одноцветным).
Однако вследствие того что точки 3 и 4 белые, точка 5 - должна быть черной (иначе треугольник (345) будет одноцветным). Далее, во избежание одноцветного треугольника (156) точку 6 нужно делать белой.
И тут мы приходим к противоречию. Точка 7 (на рисунке означена крестиком)не может быть "покрашена" в соответствии с нашим допущением
- белый цвет даст нам одноцветный ∆(637)
- черный цвет даст нам одноцветный ∆(527)
Мы пришли к противоречию. Следовательно, предположение неверно, и при любой "раскраске" всегда найдутся три одноцветные вершины, образующие равносторонний треугольник
При выборе других 2 вершин одного цвета или белого цвета вместо черного - доказательство абсолютно аналогично.
Ч.т.д.
Результат:
41.53 ≈ 42
Необходимо округлить до целого (до единиц), значит после точки мы оставляем 0 цифры.
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.
41.|53
Если справа от красной черты, стоит цифра: 0, 1, 2, 3, 4 то тогда необходимо просто отбросить все цифры стоящие после красной черты, а если стоит цифра: 5, 6, 7, 8, 9 то тогда необходимо тоже отбросить все цифры стоящие после красной черты и к цифре стоящей слева от красной черты прибавить число 1.
После красной черты у нас стоит цифра 5, значит мы должны отбросить все цифры стоящие после красной черты и прибавить 1 к цифре слева от красной черты.
41 + 1 = 42
41.53 ≈ 42
Боже осы обажаю алгебру