Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через , другой - через .
Задача сводится к нахождению p, q, r, s. Тогда
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).
Сумма корней:
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).
C^4 - 27C = C * ( C^3 - 27) = C * ( C - 3 ) * ( C^2 + 3C + 9)
25 - C^2 = ( 5 - C ) * ( 5 + C )
Y = 2X - 2 Графиком является прямая линия. Для построения достаточны две точки Точка С ( 0 ; - 2 ) и B ( 1 ; 0 ) Соединяем указанные точки. Это и есть график функции Y = 2X - 2 Проходит ли точка А ( - 10 ; - 20 ) через данный график? Y = 2X - 2 - 20 ≠ 2 * ( - 10) - 2 - 20 ≠ - 22 Равенство неверное, поэтому данная точка не проходит через указанный график
Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через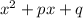
, другой - через 
.
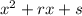Задача сводится к нахождению p, q, r, s. Тогда
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
Сумма корней: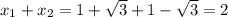
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
Сумма корней: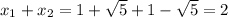
ответ: 2.