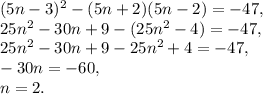
1) (5N - 3)^2 = 25N^2 - 30N + 9
2) (5N +2)*(5N-2) = 25N^2 - 4
3) 25N^2 - 30N + 9 - 25N^2 + 4 = -47
- 30N + 13 = - 47
- 30N = - 60
N = 2
ОТВЕТ: N = 2
В решении.
Объяснение:
1) (х - 4)/5 < (2х + 4)/9 + 9
Умножить все части неравенства на 45, чтобы избавиться от дробного выражения:
9*(х - 4) < 5*(2x + 4) + 45*9
9x - 36 < 10x + 20 + 405
9x - 10x < 425 + 36
-х < 461
x > -461
При х > -461 первое выражение меньше второго.
2) (х + 17)/5 = 3(х - 5)/4
Умножить все части уравнения на 20, чтобы избавиться от дробного выражения:
4*(х + 17) = 5*3(х - 5)
4х + 68 = 15х - 75
4х - 15х = -75 - 68
-11х = -143
х = -143/-11
х = 13.
При х = 13 первое выражение не больше второго (равно ему).
А х км В
> (15 + 3) км/ч 3 ч < t < 4 ч (15 - 3) км/ч <
Пусть х км - расстояние между пунктами, тогда (15 + 3) = 18 км/ч - скорость лодки по течению, (15 - 3) = 12 км/ч - скорость лодки против течения.
Составим двойное неравенство по условию задачи:
3 < х/18 + х/12 < 4
Приведём все части двойного неравенства к общему знаменателю 36
(3·36)/36 < (2х)/36 + (3х)/36 < (4·36)/36
108/36 < (5x)/36 < 144/36
108 < 5x < 144
Разделим все части двойного неравенства на 5
108 : 5 < 5x : 5 < 144 : 5
21,6 < x < 28,8
ответ: на расстояние больше 21,6 км, но меньше 28,8 км.
Проверка:
21,6 : 18 = 1,2 ч - от А до Б
21,6 : 12 = 1,8 ч - от В до А
1,2 ч + 1,8 ч = 3 ч - время в пути
28,8 : 18 = 1,6 ч - от А до В
28,8 : 12 = 2,4 ч - от В до А
1,6 ч + 2,4 = 4 ч - время в пути