
Графиком линейной функции является прямая.
х - независимая переменная, то есть может принимать любые значения.
у - зависимая переменная, то есть её значение зависит от значения х.
Чтобы построить график, возьмём две точки.
Если х = 0, у = 2
Если х = 1, у = 3
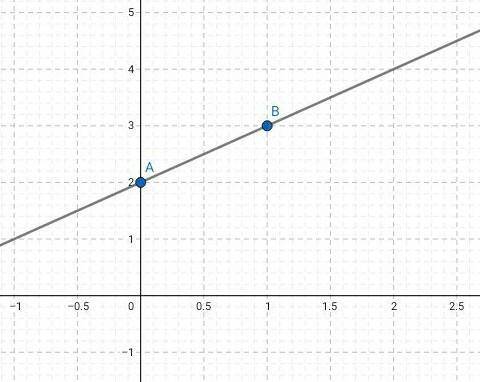
У нас есть координаты двух точек А (0;2), В (1;3). Теперь, построим график:
Задание#2А) Если х = 3 то у = 3 + 2 = 5
ответ: у = 5
Б) Если у = 0, то х:
0 = х + 2
-х = 2
х = -2
ответ: х = -2
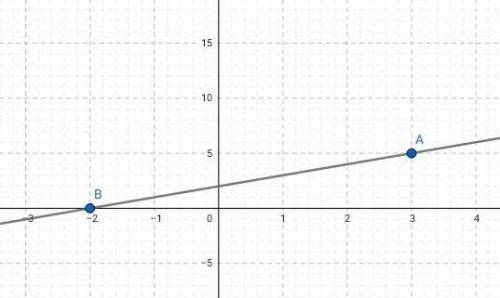
Если нужен график точек А (3;5) и В (-2;0), то он тоже прикреплен 2 картинкой.
sin2x - (1-sin²x) =0 ;
2sinxcosx -cos²x =0 ;
cosx(2sinx -cosx) =0 ;
[cosx =0 ;2sinx-cosx =0.⇔ [cosx =0 ;sinx=(1/2)cosx.⇔[cosx =0 ;tqx=1/2.
[ x=π/2 +πn ; x =arctq1/2+πn , n∈Z.
2) ;
ctq2x*cos²x - ctq2x*sin²x =0 ;
ctq2x*(cos²x - sin²x) =0 ;
ctq2x*cos2x =0 ;
sin2x =0 * * *cos2x = ± 1 ≠0→ ОДЗ * * *
2x =πn , n∈Z ;
x =(π/2)*n , n∈Z .
3) ;
3sin²x/2 -2sinx/2 =0 ;
3sinx/2 (sinx/2 -2/3) =0 ;
[sinx/2 =0 ; sinx/2 =2/3 .⇒[x/2 =πn ; x/2= arcsin(2/3) +πn ,n∈Z.⇔
[x =2πn ; x= 2arcsin(2/3) +2πn ,n∈Z.
4) ;
* *cos2α =cos²α -sin²α =cos²α -(1-sin²α)=2cos²α -1⇒1+cos2α=2cos²α * *
cos3x = 1+cos2*(3x) ; * * * α = 3x * * *
cos3x = 2cos²3x ;
2cos²3x -cos3x =0 ;
2cos3x(cos3x -1/2) =0 ;
[cos3x =0 ; cos3x =1/2 ⇒[3x=π/2+πn ; 3x= ±π/3+2πn ,n∈Z.⇔
[x=π/6+πn/3 ; x= ±π/9+(2π/3)*n ,n∈Z.