1) c² + b³ - cb + c - cb² - b² = (c² - cb + c) + (b³ - cb² - b²) =
= c(c - b + 1) + b²(b - c - 1) = c(c - b + 1) - b²( c - b + 1) = (c - b + 1)(c - b²)
2) (x + y - 7)² + (x - 2y + 2)² = 0
Это равенство верно только в случае, когда :
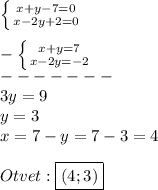
3) Пусть надо взять х кг 25% - го и y кг 50% - го сплавов меди . Надо получить 20 кг 40% - го сплава.
x y 20 = x + y
25% 50% 40%
0,25x + 0,5y = 0,4(x + y)
Если x + y = 20 , то y = 20 - x
0,25x + 0,5 * (20 - x) = 0,4 * 20
0,25x + 10 - 0,5x = 8
- 0,25x = - 2
x = 8 кг - 25% - го
y = 20 - 8 = 12 кг - 50% - го
ответ : надо взять 8 кг 25% - го и 12 кг 50% - го сплавов
Система линейных уравнений с двумя неизвестными
x + y = 5
2x - 3y = 1
Система линейных ур-ний с тремя неизвестными
2*x = 2
5*y = 10
x + y + z = 3
Система дробно-рациональных уравнений
x + y = 3
1/x + 1/y = 2/5
Система четырёх уравнений
x1 + 2x2 + 3x3 - 2x4 = 1
2x1 - x2 - 2x3 - 3x4 = 2
3x1 + 2x2 - x3 + 2x4 = -5
2x1 - 3x2 + 2x3 + x4 = 11
Система линейных уравнений с четырьмя неизвестными
2x + 4y + 6z + 8v = 100
3x + 5y + 7z + 9v = 116
3x - 5y + 7z - 9v = -40
-2x + 4y - 6z + 8v = 36
Система трёх нелинейных ур-ний, содержащая квадрат и дробь
2/x = 11
x - 3*z^2 = 0
2/7*x + y - z = -3
Система двух ур-ний, содержащая куб (3-ю степень)
x = y^3
x*y = -5
Система ур-ний c квадратным корнем
x + y - sqrt(x*y) = 5
2*x*y = 3
Система тригонометрических ур-ний
x + y = 5*pi/2
sin(x) + cos(2y) = -1
Система показательных и логарифмических уравнений
y - log(x)/log(3) = 1
x^y = 3^12
Объяснение:
Формула приведения.
Объяснение:
a) sin(π-α) = sinα
б) cos( 3π/2 + α ) = sinα