Допустим, что . Тогда имеем уравнение , не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е.
Преобразуем правую часть:
Перенесем все влево с противоположным знаком:
Поскольку , можем разделить обе части уравнения на . В итоге имеет равносильное исходному уравнение
Заметим, что является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен .
После того, как из 2-ого стакана перелили 150 мл (половину из 300мл) кофе с молоком в 1-ый стакан, во 2-ом стакане осталось: 200/2 = 100 мл кофе и 100/2 = 50 мл молока, тогда в 1-ом стакане стало: 0 + 200/2 = 100 мл кофе и 150 + 100/2 = 200 мл молока. После того, как из 1-ого стакана перелили во 2-ой 150 мл полученного напитка - половину его (после первого переливания получилось 300 мл напитка), то во 2-ом стакане стало: 100 + 100/2 = 150 мл кофе и 50 + 200/2 = 150 мл молока. Получается, что кофе и молока во 2ом стакане стало поровну. Значит содержание кофе - 50%. ответ: 50%
Допустим, что
. Тогда имеем уравнение 
, не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е.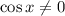 
Преобразуем правую часть:
Перенесем все влево с противоположным знаком:
Поскольку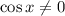
, можем разделить обе части уравнения на 
. В итоге имеет равносильное исходному уравнение
Заметим, что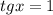
является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен 
.
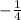Соответственно, имеем два случая: или
или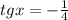 
.
1 случай.
2 случай.
Имеем две серии корней.
ОТВЕТ: π/4 + πk, k ∈ Z; -arctg(1/4) + πn, n ∈ Z.