Question

Доброго времени суток и господа, будте добры подскажите как решить : "найти значение функции у=3х^5+20х^3+3 в точке максима" . всего лишь один подробный пример и я смогу решить все остальные подобного типа, за ранее!

Answer 1

нет ничего проще.

шаг 1.

ищем производную

15x^4+60x^2

шаг 2

находим точки, где данная производная равна 0

15x^2(x^2+4)

x=0

шаг 3.

смотрим меняет ли производная знак при переходе через критическую точку

ответ нет. производная больше нуля при любых х, следовательная данная функция

может только возрастать.

у нее нет точек экстремума

Answer 2

для визуалов ))). Неудачный у вас пример, чтобы на нем осваивать остальные задания. Хотя, как знать... ))).

$y=3x^5+20x^3+3 \\\ D(y)=R \\\ y'=15x^4+60x^2=15x^2(x^2+4) \\\ y'=0, \ 15x^2(x^2+4)=0 \\\ x=0$

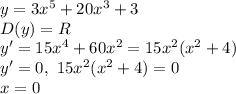
Критическая точка х=0.

     +          +

---------|--------->

           0

Т.к. в окрестности точки х=0 производная функции положительна (как слева, так и справа), то х=0 - не является точкой экстремума для функции у=3х^5+20х^3+3.

Т.е. данная функция максимума не имеет. И вычислить значение в точке максимума невозможно.