Решение Вашего задания во вложении
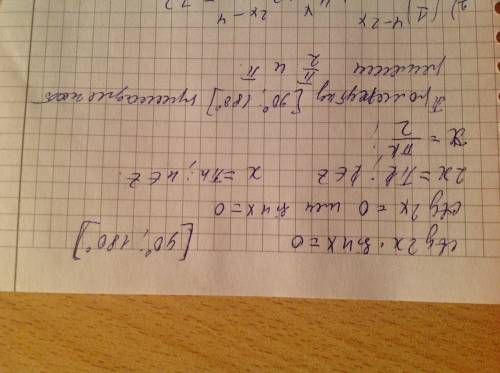
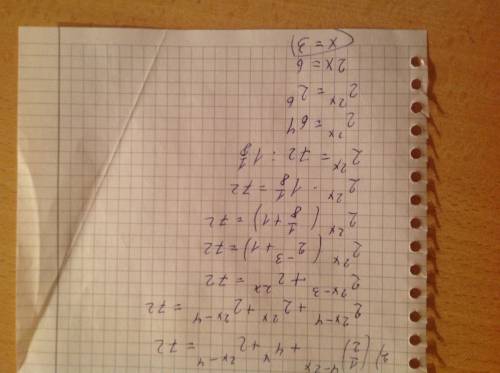
Пусть сторона квадрата х см, тогда длина прямоугольника (3х) см, а ширина прямоугольника - (х - 5) см.
Т.к. площадь квадрата находят по формуле S = а², где а - сторона квадрата, о площадь данного квадрата равна (х²) см².
А т.к площадь прямоугольника находят по формуле S = a · b, где a и b - длина и ширина прямоугольника, то площадь данного прямоугольника будет равна S = 3х · (х - 5) = 3х² - 15х (см²).
Т.к. площадь квадрата на 50 см² меньше площади прямоугольника, то составим и решим уравнение:
3x² - 15х = x² + 50,
3x² - x² - 15x - 50 = 0,
2x² - 15x - 50 = 0,
D = (-15)² - 4 · 2 · (-50) = 225 + 400 = 625 ; √625 = 25,
x₁ = (15 + 25)/(2 · 2) = 40/4 = 10,
x₂ = (15 - 25)/(2 · 2) = -10·/4 = -2,5 - не подходит по условию задачи.
Значит, сторона квадрата равна 10 см.
ответ: 10 см.
Пусть х(км/ч) -скорость течения реки.
у(км/ч) -собственная скорость катера.
Тогда скорость катера по течению реки равна (х+у) км/ч,
а против течения (у-х) км/ч.
По условию по течению катер км), т.е. 5/3 х +5/3 у(км),
а против течения 24(км), т. е. 1,5 у -1,5 х (км).
(5/3 - это 1час 20мин.)
5/3 х +5/3 у =28 домножим на 3
1,5 у-1,5 х=24 домножим на 10
5х+5у=84
15у-15х=240 разделим на 3
5х+5у=84
5у-5х=80
Решим систему сложения двух уравнений:
10у = 164
5у-5х = 80
5у - 5х = 80
у = 16,4
5*16,4 - 5х = 80
у=16,4
-5 х = 80-82
у = 16,4
-5 х = -2
у = 16,4
х = 0,4
у = 16,4
ответ: 0,4 (км/ч) - скорость течения реки
№1 ctg2x*sinx=0
ctg2x=0
cos2x=0, при этом sin2x=\=0
2x=+-pi/2+2pik
x=+pi/4+pik
sinx=0
x=pi+pik
pi/2<=pi/4+pik<=pi
1/2<=1/4+k<=1
1/4<=k<=1
k=1 => x=pi/4+pi=5pi/4
1/2<=-1/4+k<=1
3/4<=k<=1
k=1 => x=-pi/4+pi=3pi/4
1/2<1+k<=1
-1/2<=k<=0
k=0 => x=pi
№2 (1/2)^4-2x+4^x+2^2x-4=72
Скорее всего уравнение записано неверно, т.к. реальных корней нет