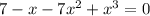
81/4y^2t^6m^2
Объяснение:
Пример 5 - Для начала сделаем из неправильной дроби правильную. 1/2 - 1: числитель. 2: знаменатель. 4: целое число.
Целое число умножаем на знаменатель, а после полученное число прибавляем к числителю.
4*2 = 8, 8+1=9
числитель по правилу ставим полученное нами число, а знаменатель остается тот же.
И того 9/2
Чтобы возвести это число в указанную нам степень, нужно и 9 и 2 отдельно умножить на себя два раза.
То есть 9*9=81 2*2=4
Такие числа как y без указанной степени уже имеют степень 1. При умножении степеней за скобкой, следует правило умножения. Соответственно, y^2.
t^3 степени умножить на 2 - 3*2=6
Соответственно t^6.
m^1 умножить на степень 2 - 1*2=2
Объяснение:
x²+2x+1>0
Допустим x²+2x+1=0; D=4-4=0
x=-2/2=-1
Отсюда следует, что значение корня повторяется два раза. Значит, знак при переходе через число -1 не будет меняться:
+ +
°>x
-1
Выбираем нужные интервалы со знаком плюс и получаем:
x∈(-∞; -1)∪(-1; +∞).
x-x²-5≥0 |×(-1)
x²-x+5≤0
Допустим x²-x+5=0; D=1-20=-19 - D<0 - уравнение не имеет решений, значит, данное неравенство выполняется всегда или не выполняется никогда.
Возьмём произвольную точку, например, 0:
0-0²-5=-5; -5<0
Неравенство не выполняется ⇒ данное неравенство не имеет решений.
7-х-7х²+х³=0
7-х-х²•(7-х)=0
(7-х)•(1-х²)=0
7-х=0
1-х²=0
х=7
х=-1
х=1
х1=-1, х2=1, х3=7