|y
|x
| .
| .
| .
| .
| .
| .
0
(ось у сплошной. соединишь точки - получишь график - ветвь параболы, лежащая на боку)
а) наиб. и наим. значение находим через производную
(-√x)'=-1/(2√x)
приравниваем к нулю -1/(2√x)=0. нет корне. находим значение функции на концах отрезка.
y(1)=-1
y(6)=-√6
-1 наиб. знач.
б) так как пересекаются, значит х1=х1, у1=у2
y*y+3+4y=0
D=16-12=4
y1=(-4+2)/2=-1
y2=-3
оба подходят
находим х1 и х2
х1=1
х2=9
ответ:а)-1, б)(1;-1), (9:-3).
График построен, смотрите во вложениях.
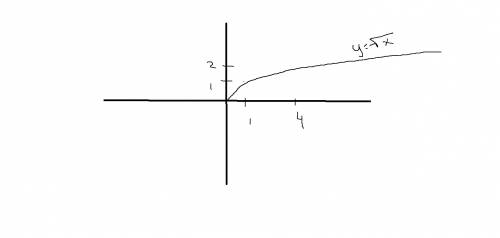
а) наименьшее и наибольшее значение можно посмотреть по графику
Наименьшее y=2;
Наибольшее y=sqrt(7) (sqrt(число) - корень квадратный из числа)
б)Координаты пересечения с прямой х-2γ=0
Для начала, приведем эту прямую к нормальному виду.
2y=x
y=x/2
Теперь посмортим на его свойства, это прямая, проходящяя через начало координат, точка(0;0) (уже 1 точка) и через точку (4;2) черет эту же точку проходит и наш график y=sqrt(x)
Значит всего 2 точки пересечения (0;0) и (4;2)
Почему нету больше точек? Если построить график функции прямой, то мы увидим что она гараздо прогрессивней идет вверх че sqrt(x) , значит они бошльше не пересекуться, и точек пересечения не будет.
х = 2, у = -5
Объяснение:
В точке пересечения графиков функций координаты равны.
1) Запишем исходные уравнения в следующем виде:
у – х = -7
у = х - 7
и
2x + y= -1
у = -2х - 1
2) Так как
х- 7 = -2х -1,
то х + 2х = 7 - 1
3 х = 6
х = 6 : 3
х = 2
3) Находим координату у для первой прямой:
у = х - 7 = 2 - 7 = - 5.
4) Находим координату у для второй прямой:
у = -2х - 1 = - 2 · 2 - 1 = - 5
Значения совпали, значит координаты точки пересечения найдены верно.
ответ: координаты точки пересечения прямых у – х = -7 и 2x+y= -1:
х = 2, у = -5.