Теорема (Достаточный признак монотонности).
1) Еслипроизводная f ' (x) от ф-ии f(x) всюду в интервале положительна, то
ф-ия f(x) в этом интервале возрастает;
2) Если производная f " (x) от ф-ии f(x) всюду в интервале отрицательна, то
ф-ия f(x) в этом интервале убывает;
3) Если производная f " (x) от ф -ии f(x) всюду в интервале равна нулю,
то ф-ия f(x) в этом интервале не изменяется ( есть константа).
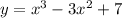
1. Функция многочлен, а значит область определения функции вся вещественная ось.
2. Многочлены будут четными, если содержат только четные степени переменной и наоборот нечетными при нечетных степенях. в нашем случае функция является ни четноой, ни нечетной. Функция непериодическая.
3. Функция не имеет асимптот.
4. Поскольку функция имеет степень 3, то ее график не имеет ни горизонтальных, ни наклонных асимптот.
5. найдем пересечение с осью Оу для этого найдем значене у при х=0
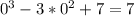
и пересечение с осью Ох для этого решим уравнение 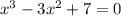
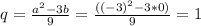
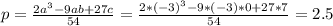
получаем каноническое уравнение
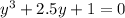
найдем Q
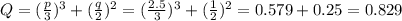
так как Q>0, то по методу Кардано уравнение имеет один действительный корень
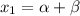
![\alpha=\sqrt[3]{-\frac{q}{2}+\sqrt{Q}}=\sqrt[3]{-\frac{1}{2}+\sqrt{0.829}}](/tpl/images/0172/1280/2c7f2.png)
![\beta=\sqrt[3]{-\frac{q}{2}-\sqrt{Q}}=\sqrt[3]{-\frac{1}{2}-\sqrt{0.829}}](/tpl/images/0172/1280/5f9bf.png)
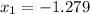
6. производная функции будет 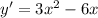
найдем интервалы возрастания и убывания
решим неравенство 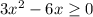
решим квадртное уравнение
дискриминант будет равен 36
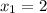
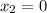
следовательно на интервалах ]-∞;0] и [2;+∞[ функция возрастает, а между ними функция убывает
и в итоге строим график

y будет иметь минимум в точке где знаминатель дроби максимальный.
квадратный трехчлен с отрицательным первым множителем максимален в вершине
-b/2A=a/2
найдем множетель а, для чего подставим точку в внашу функцию
-1/11=1/(-9-4-3a)
1/11=1/(13+3a)
13+3a=11
3a=-2
a=-2/3
найдем значение в точке х=-1/3
1/(1/9+2/9-4)=-3/11