1)Т.к. (пи/2<альфа<пи) ---> 2 четверть в окружности значит cos будет с минусом. Теперь находим cos по тождеству: cos^2 альфа+sin^2 альфа=1 cos^2 альфа=(1/1)-(64/289), т.е. синус возвела в квадрат и перенесла знак меняется, теперь приводим к общему знаменателю, т.е. 289 домнажаем дроби и получаем: (225/289), это получается cos с минусом и выводим из квадрата и получаем: cos альфа = (-15/17); 2)-а: tg альфа = (sin альфа/cos альфа) ctg альфа = (cos альфа/sin альфа) подставляешь и получаешь: 1-sin^2 альфа, из тождества (cos^2 альфа+sin^2 альфа=1) выражаем и получаем: cos^2 альфа=1-sin^2 альфа; 3)-а: (1+tg^2 альфа это отношение : 1/cos^2 альфа, значит: 1/cos^2 альфа*cos^4 альфа/1 + sin^2 альфа (сокращаем и получаем): cos^2 альфа+sin^2 альфа=1, т.к. это основное тождество.
Объяснение:
2.
a) 3x+12>4x-1 | (-x>-13) /-1 | x<13
7-2x<=10-3x | -3 <= -x /-1 | x <= 13. x принадлежит (-∞; 13].
б) 2x-9 > 6x+1 | (-4x > 10) / -4 | x<10
( -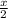 < 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
< 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
3.
а)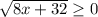 Взводим все в квадрат
Взводим все в квадрат
8x+32 => 0
8x => 32 делим все на 8
x => 4. x принадлежит [4; +∞).
б)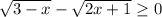 Взводим все в квадрат
Взводим все в квадрат
3-x-2x+1 => 0
4 => 3x Делим все на 3
1.3 => x
x <= 1.3. x принадлежит [-∞; 1.3).
4.
а-7 => 0 3-2a => 0
a => 7 3 => 2a
1.5 => a ответ: a принадлежит [7; +∞).