![x^3+3x+2\sqrt[3]{x-4} -34=0](/tpl/images/1360/1028/6c477.png)
Запишем уравнение в виде:
![x^3+3x -34=-2\sqrt[3]{x-4}](/tpl/images/1360/1028/bd4bd.png)
Пусть левая и правая часть равны у. Тогда получим систему:
![\begin{cases} y=x^3+3x -34\\y=-2\sqrt[3]{x-4}\end{cases}](/tpl/images/1360/1028/c1e6e.png)
Рассмотрим каждое уравнение как функцию.
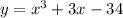- возрастающая функция, так как это кубическая парабола с положительным старшим коэффициентом
![y=-2\sqrt[3]{x-4}](/tpl/images/1360/1028/0df79.png)
- убывающая функция, так как корень нечетной степени имеет сомножителем отрицательное число
Графически возрастающая и убывающая функция могут пересекаться не более чем в одной точке.
В данном случае, понимая, что и область определения и область значений каждой функции представляют собой все действительные числа можно сказать, что такое пересечение обязательно произойдет.
Таким образом, если найден некоторый корень этого уравнения, то других корней у уравнения нет.
Подберем корень. Удобно начать проверку с "красивых значений". Например, будем выбирать х так, чтобы под знаком корня получался куб некоторого целого числа.
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{0}](/tpl/images/1360/1028/d91f8.png)
, то есть 
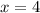. Проверим, является ли это число корнем:
![4^3+3\cdot4+2\sqrt[3]{4-4} -34=64+12+2\cdot0-34=42\neq 0](/tpl/images/1360/1028/6e40b.png)
- не корень
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{1}](/tpl/images/1360/1028/7bd4a.png)
, то есть 
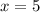. Проверим, является ли это число корнем:
![5^3+3\cdot5+2\sqrt[3]{5-4} -34=125+15+2\cdot1-34=108\neq 0](/tpl/images/1360/1028/f1f89.png)
- не корень
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{-1}](/tpl/images/1360/1028/4572f.png)
, то есть 
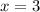. Проверим, является ли это число корнем:
![3^3+3\cdot3+2\sqrt[3]{3-4} -34=27+9+2\cdot(-1)-34=0](/tpl/images/1360/1028/fd423.png)
- корень
Таким образом, уравнение имеет единственный корень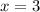
ответ: 3
а) Точки, лежащие на оси Ox, имеют ординату, равную нулю. Значит, вторая координата вектора OM равна 0.
б) Точки, лежащие на оси Oy, имеют абсциссу, равную нулю. Значит, первая координата вектора OM равна 0.
в) Точки, лежащие в 1 четверти, имеют положительные абсциссу и ординату. Значит, координаты вектора OM положительны.
г) Точки, лежащие во 2 четверти, имеют отрицательную абсциссу и положительную ординату. Значит, первая координата вектора OM отрицательна, а вторая - положительна.
д) Точки, лежащие в 3 четверти, имеют отрицательные абсциссу и ординату. Значит, координаты вектора OM отрицательны.
е) Точки, лежащие в 4 четверти, имеют положительную абсциссу и отрицательную ординату. Значит, первая координата вектора OM положительна, а вторая - отрицательна.
D=25+4*3*2=7^2
x1=-2/4=-1/2
x2=12/4=3