Воспользуемся формулой 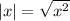 :
:
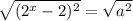
Возведем обе части в квадрат:
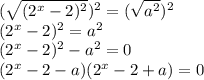
Рассмотрим 3 случая :
1.
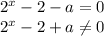
----------------------
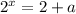
Мы знаем, что любое число(кроме 0) в любой степени больше нуля, то есть 2+а > 0 => a>-2
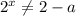
Так же 2-а уже должно быть меньше или равно нулю:
2-a ≤ 0 => a ≥ 2
Найдем пересечение => a ≥ 2
2.
По тому же принципу :
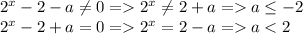
Найдем пересечение => a ≤-2
3.
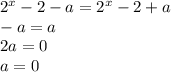
----------------------------------------------------------------------
Объединим три ответа => a Є (-∞ ; -2] U [2 ; +∞)
ответ : a Є (-∞ ; -2] U [2 ; +∞) U {0}
P.S это одно из возможных решений, возможно вы найдете и по проще)
ненулевой остаток от деления на 4 может быть равен 1, 2 или 3.
если при делении на 15 остаток такой же, то и при делении на 60 тоже.
значит, это трехзначное число, которое можно представить как
100a + b + c = 60p + 1; или 60p + 2; или 60p + 3.
так как 60 делится на 10, то c = остатку, 1, 2 или 3.
и это число с есть среднее арифметическое чисел a и b.
если с = 1, то a = b = 1, но число 111 при делении на 60 дает остаток 51.
если с = 2, то а = 3, b = 1, или наоборот, a = 1, b = 3, или a = 4, b = 0.
но числа 132, 312 и 402 тоже не те остатки.
значит, c = 3. тогда возможны такие пары:
(a; b) = (4; 2); (2; 4); (1; 5); (5; 1); (6; 0)
из чисел 420, 240, 150, 510, 600 только 240 и 600 делятся на 60.
ответы: 243 и 603
а) 128a⁴ - 18b² = 2(64a⁴ - 9b²) = 2(8a² - 3b)(8a² + 3b)
б) 99x² - 132xy + 44y² = 11(9x² - 12xy + 4y²) = 11(3x - 2y)²