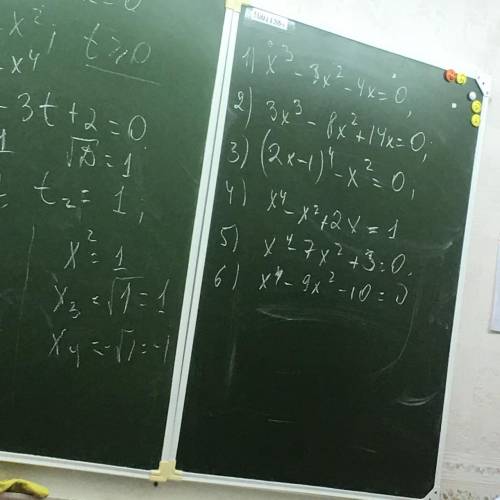
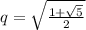
 - k-ый ((n-k)+1)-ый
- k-ый ((n-k)+1)-ый  - (k+1)-ый (n-k)ый
- (k+1)-ый (n-k)ый - n-ый обратный счет вверх 1-ый
- n-ый обратный счет вверх 1-ый 
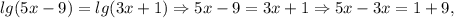
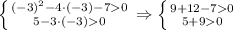
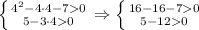
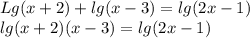 заменили сумму логарифмов логарифмом произведения.
заменили сумму логарифмов логарифмом произведения.
Объяснение:
1) x^3-3x^2-4x=0 2)3x^3-8x^2+14x=0
x(x^2-3x-4)=0 x(3x^2-8x+14)=0
X1=0 (x^2-3x-4)=0 Х1=0 (3x^2-8x+14)=0
X2,3=(3±√9+16)/2 X2,3=(8±√64-168 Дискриминант∠ 0
X2=4 X3=-1 Корней Х2,3 нет
Отв: X1=0 X2=4 X3=-1 Отв. Х1=0
3)(2х-1)^4-x^22=0 4) x^4-x^2+2x=1
((2x-1)^2-x)((2x-1)^2+x)=0 x^4-x^2+2x-1=0
(4x^2-4x+1-x)(4x^2-4x+1+x)=0 x^4-(x^2-2x+1)=0
(4x^2-5x+1)(4x^2-3x+1)=0 x^4 -(x-1)^2=0
X1,2=(5±√25-16)/8 (x^2-x+1)(x^2+x-1)=0
x1,2=(5±3)/8 x1,2=(1±√1-4 D∠0 КОРНЕЙ НЕТ
x1=1 X2=0,25 х3,4=(-1±√1+4)/2
x3,4=3±√9-19 X3=(-1÷√5)/2 X4=(-1-√5)/2
D∠0 корней Х3 и Х4 нет
Отв. Х1=1 Х2=0,25 Отв. X3=(-1÷√5)/2 X4=(-1-√5)/2
5) x^4-7x^2+3=0 6)x^4-9x^2-10=0 x^2=t, t≥0
x^2=t, t≥0 t^2-9t-10=0
t^2-7t+3=0 t1,2=(9±√81=40)/2
t=(7±√49-12)/2 t=(7±√37)/2 t=(9±11)/2
X^2=(7±√37)/2 9-11/2∠0 t=20
X1=±√(7+√37)/2 x^2=10 X=±√10
X2=±√(7-√37)/2 Отв. х=±√10
Отв.X1=±√(7+√37)/2
X2=±√(7-√37)/2