ответ:
x∈(-∞; -6)∪(6; 10]
объяснение:
(x^2-16x+60)/(x^2-36)≤0
y=(x^2-16x+60)/(x^2-36)
(x^2-16x+60)/(x^2-36)=0
1) x^2-16x+60=0
d=256-4*60=256-240=16
2) x^2-36≠0
x^2≠36
x≠6
x≠-6
- + - +
---()()*>
(-6) (6) 10
x∈(-∞; -6)∪(6; 10]
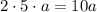
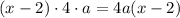

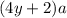 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: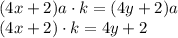
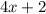 и выражение
и выражение 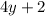 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном  возникает противоречие:
возникает противоречие:
х=53,5:5
х=25,7
7*х=1,75
х=1,75:7
х=0,25
21,71+4,06*х=27,8
4,06*х=27,8-21,71
4,06*х=6,09
х=6,09:4,06
х=1,5