ответ:1)правильно
2)правильно
3)неправильно
4)правильно
Объяснение:
3.. мы знаем, что в десятичных дробях мы можем поставить в конце нуль, много нулей и значение все равно не изменится
если тебе будет проще, то составь координатную прямую
>
-1.3 -1.2 0
а) -1,15
давайте -1.3 и -1.2 запишем как -1.30 и -1.20
>
-1.30 -1.20 -1.15
не подходит
б) -1.25
снова представляем числа в условии с двумя знаками после запятой
это число заключено между числами из условия
в) -1,4
не включено
г) -1.263
представим числа из условия таким образом -1.300 и -1.200
число подходит
4. давайте попробуем опять воспользоваться координатной прямой
>
-900 -800
помним, что чем больше модуль отрицательного числа (число просто, без минуса), тем оно левее, меньше
-839 должно быть больше -900 и при этом меньше -800
на координатной прямой это выглядит примерно так
>
-900 -839 -800
так что, неравенство верно
5. знаки ≥ и ≤ обозначают (больше или равно/меньше или равно) у нас в условии нет того, что числа равны, так что первое и последнее сразу не подходит
"а" находится между 3.5 и 4.6
букву ставим в середину неравенства и получается
3.5<а<4.6
знаки неравенства направлены в сторону "а" , можно увидеть, что первый знак обозначает что а больше 3.5 , а второй что а меньше 4.6
значит, ответ третий
1) a)y=3 б)x=3 в) (3;+∞) возрастает (-∞;3) убывает
2)а)у=-0,5 б) у=0,25 в) у=3
3) у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Объяснение:
1) находим по графику абсцисса -это х ордината это -у
2)подставляем вместо х значение и считаем
3) a)у(4)=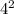 =16 б)у(-3)=
=16 б)у(-3)=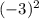 =9 в) у(2)=
=9 в) у(2)=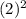 =4
=4
у(3)=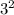 =9 у(-2)=
=9 у(-2)=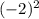 =4 у(-5)=
=4 у(-5)=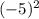 =25
=25
у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Верно: 1, 4
Неверно: 2, 3
Объяснение: