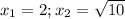Объяснение:
1. ОДЗ отобразим по мере необходимости.
x²/(x+6)=1/2
2x²=x+6
2x²-x-6=0; D=1+48=49
x₁=(1-7)/4=-6/4=-3/2
x₂=(1+7)/4=8/4=2
ответ: -3/2; 2.
(x²-x)/(x+3)=12/(x+3) |×(x+3)
x²-x-12=0; D=1+48=49
x₁=(1-7)/2=-6/2=-3 - корень не подходит, так как x+3≠0; x≠-3.
x₂=(1+7)/2=8/2=4
ответ: 4.
y=(x²-3x+2)/(x²-1), где x²-1≠0 ; x²≠1; x≠±√1; x≠±1
x²-3x+2=0; D=9-8=1
x₁=(3-1)/2=2/2=1 - этот корень не подходит.
x₂=(3+1)/2=4/2=2
ответ: 2.
y=(x²-5x+6)/(x²-4), где x²-4≠0; x²=4; x≠±√4; x≠±2
x²-5x+6=0; D=25-24=1
x₁=(5-1)/2=4/2=2 - этот корень не подходит.
x₂=(5+1)/2=6/2=3
ответ: 3.
Пусть большее простое число из T(x) равно n.Сравним числа:n^2 и 2T(x),то есть квадрат наибольшего простого числа и удвоенную сумму простых чисел до n:
Очевидно,что все простые числа,кроме 2 нечетные,а значит T(x) меньше суммы двойки и натуральных нечетных чисел от 1 до n(так как не все нечетные числа являются простыми).
Рассмотрим данную сумму,члены которой,кроме двойки образуют арифметическую прогрессию.
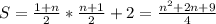
Сравним 2S и n^2
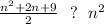


Правая часть больше левой(нуля) при:

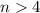
А так как S>T(X) и n^2>2S,то n^2>2T(x)
Значит и x^2>2T(x) при n,указанном выше.
Рассмотрим оставшиеся 2 варианта:
n=2 n=3

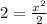


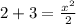
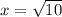
ответ: