Докажем вначале важное утверждение которым и воспользуемся.
Утверждение:
Пусть А - непустое и не конечное множество, так что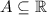 
. Предположим что существует 
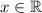так что 
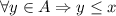. Если существует последовательность 
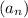элементов из А выполняющая 
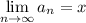то 
.
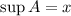Доказательство:
Допустим от противного, что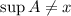 
, тогда существует 
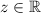так что 
.
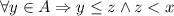Из-за того что 
, обязательно выполняется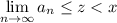 
что противоречит тому что 
.
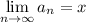Следовательно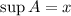 
.
Существует эквивалентное утверждение связанное с инфимумом, но доказывать его не буду (оно аналогично доказательству, но с некоторыми изменениями).
Теперь решим саму задачу:
Заметим что данное множество состоит из элементов последовательности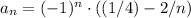 
, а также тот факт что для всех 
:
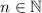Т.е.:
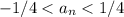
Рассмотрим две подпоследовательности -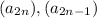 
Так как:
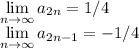
Получаем: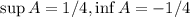 
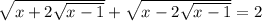
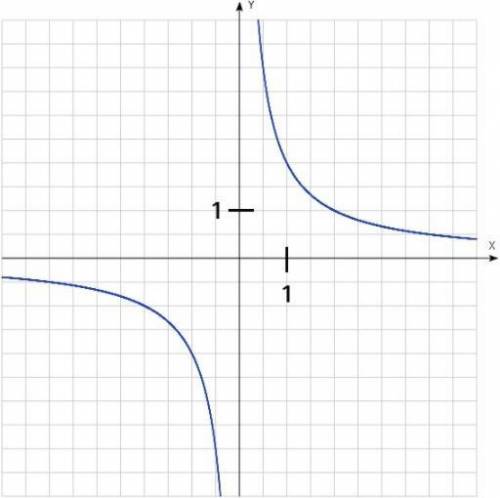
Если k>0, то график находится в 1-м и 3-м углах.
Если k<0, то график находится во 2-м и 4-м углах.
Объяснение:
Берем точку, принадлежащую графику. Например: (2;1)
х=2, у=1 подставляем в у=kx. 1=k·2 ⇒ k=1/2 >0