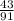
Объяснение:
Всего шаров 6+8 = 14
Вероятность того, что первый шар будет черным:
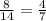
После того, как вынули черный шар, в ящике осталось 13 шаров, из которых 7 черных.Теперь вероятность того, что вытянутый шар будет черным:
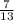
Вероятность того, что оба вынутых шара будут черными:
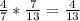
Теперь вычислим вероятность вынуть два белых шара.
Вероятность вынуть белый шар:
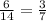
Вероятность вынуть второй белый шар:
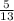
Вероятность того, что оба вынутых шара будут белыми:
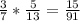
Теперь наконец-то вычислим вероятность того, что вынут два шара одного цвета (т.е. вынут два черных шара или два белых шара), используя правило сложения:
 .
.
-1010
Объяснение:
Ну тут все просто рассмотри каждые суммы по 2 слогаемых, 1-2=-1, 3-4=-1, 5-6=-1. и так далее, т.е. каждый раз мы складываем -1, теперь нужно понять сколько раз мы сложили, очевидно мы складываем пары, а чисел у нас 2020, значит пар у нас 2020/2=1010, умножаем 1010 на -1, получаем ответ.
Второй : сгруппируем слогаемые так, чтобы мы складывали 1+3+5+7, т.е. сумма всех нечетных до 2019, а в оставшейся группе вынесем минус, тогда получится сумма всех четных до 2020. И нужно из суммы всех нечетных вычесть сумму всех нечетных, но вопрос как эти суммы посчитать? ответ - воспользуемся формулой арифмитической прогрессии. Арифм. прог - последовательность чисел, которые отличаются друг от друга на одно и то же число, называемое разностью.
Тогда сумма первых эн членов арифмитической прогрессии равна
удвоенный первый член+ разность прогрессии умножить на кол-во слогаемых минус 1 ,разделить это пополам и умножить на кол-во пар.
Sn=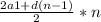
1-ые члены известны для каждой группы, это единица и двойка. разности тоже одинаковы, и равны двум(т.к. 3-1=2 и 4-2=2)
А вот сколько слогаемых?. Четных и нечетных чисел равное количество от 2020, значит четных 1010 и нечетных столько же
Тогда Сумма четных 2*1+2(1010-1)*1010/2=(1+1009)*1010=1020100
Сумма нечетных 4+2(1010-1)*1010/2=(2+1009)*1010=1021110
Вычитаем из первой суммы вторую и получаем -1010