Question

Задание 1.Задана функция:  y= х2+2+6х                                                                                                                                                                       1.     Записать коэффициенты a, b, c
2.     Определить координаты вершины параболы.
3.     Найти значения функции при:
            х= -1; 1; - 5; -7                                                                                                          
4.     Построить график функции.
5.     Определить значения аргумента функции при:
         f(x) = -3                                                                                                                                                                    
6.     Найти наименьшее и наибольшее значение функции на отрезке:  [-4; 0]                                                                                                                                
7. Указать участки возрастания и убывания функции

сможете ответить за короткое время у меня сор​

Answer 1

$y=x^2+6x+2\\\\1.\ \ a=1\ ,\ \ b=6\ ,\ \ c=2\\\\2.\ \ x_{v}=-\dfrac{b}{2a}=-\dfrac{6}{2}=-3\ \ ,\ \ y_{v}=y(-3)=9-18+2=-7\ \ ,\ \ V(-3;-7)\\\\3.\ \ y(-1)=1-6+2=-3\ \ ,\ \ y(1)=1+6+2=9\ \ ,\\\\y(-5)=25-30+2=-3\ \ ,\ \ y(-7)=49-42+2=9\\\\5.\ \ f(x)=-3\ \ \to \ \ x^2+6x+2=-3\ \ ,\ \ x^2+6x+5=0\ \ \to \\\\{}\qquad x_1=-5\ ,\ x_2=-1\ \ \ \ (teorema\ Vieta)\\\\6.\ \ x\in [-4\ ,\ 0\ ]:\ y_{naimen.}=y(-3)=-7\ ,\ \ y_{naibol.}=y(0)=2\\\\7.\ \ y(x)\ vozrasnaet:\ x\in [-3;+\infty )$

    $y(x)\ ybuvaet:\ x\in (-\infty;-3\ ]$

Answer 2

Дана функция y = x² + 2 + 6x

Перепишем ее в более удобном виде:

y = x² + 6x + 2

1. Для квадратного уравнения воспользуемся шаблоном:

ax² + bx + c = 0

Найдем коэффициенты:

a = 1;

b = 6;

c = 2;

2. Определим вершины по заданной формуле:

$x_{0} = \frac{-b}{2a}$

Подставим значения, найденные в пункте:

$x_{0} = \frac{-6}{2} = -3$

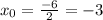
Подставим в изначальную формулу и найдём координату y вершины:

$y_{0} = (-3)^2 + (-3 * 6) + 2 = 9 - 18 + 2 = -7$

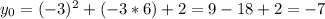
Запишем полученные данные

(-3; -7);

3.

Подставим значения в формулу:

$1) x = -1; y = (-1)^2 - 6 + 2 = 1 - 6 + 2 = -3$

$2) x = 1; y = (1)^2 + 6 + 2 = 1 + 8 = 9$

$3) x = -5; y = (-5)^2 - 5 * 6 + 2 = 25 - 30 + 2 = -3$

$4) x = -7; y = (-7)^2 - 7 * 6 + 2 = 49 - 42 + 2 = 9$

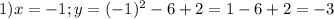
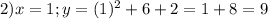
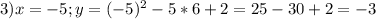
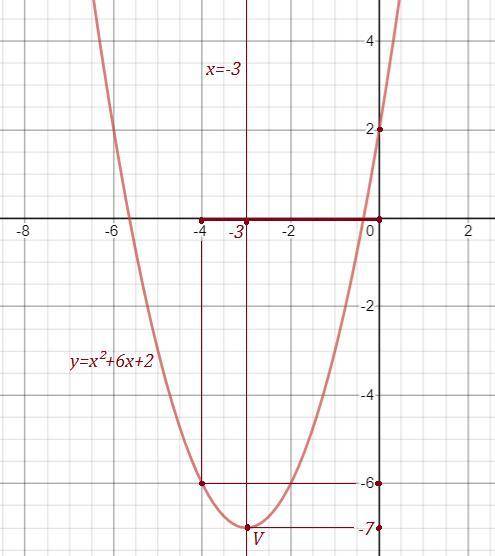
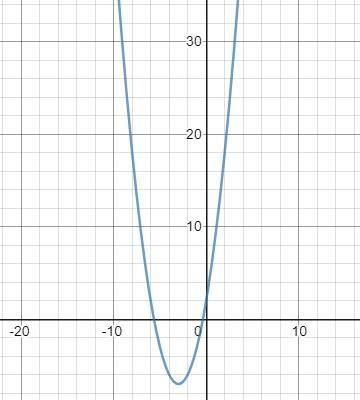
4. (График в прикрепленном файле)

5. Подставим значения:

$x^2 + 6x + 2 = -3$

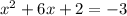
Перенесем "-3":

$x^2 + 6x + 5 = 0$

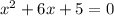
Решим квадратное уравнение:

$D = b^2 = 4ac = 36 - 4 * 1 * 5 = 16$

$x_{1} = \frac{-b + \sqrt{D}}{2a} = \frac{-6 + 4}{2} = -1$

$x_{2} = \frac{-b - \sqrt{D}}{2a} = \frac{-6 - 4}{2} = -5$

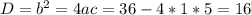
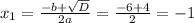
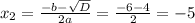
6. По графику функции видно, что наибольшее значение на этом значении при x = 0, а наименьшее это вершина:

$y_{min} = -7$

$y_{max} = 0 + 2 + 0 = 2$

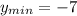
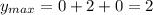
7. С обозначения параболы выплывает, что участок возрастания это все после вершины, а участок убывания до. Тогда:

Возрастания : (-3; +∞)

Убывания: (-∞; -3)