По условию, выражение -5с-с² принимает отрицательные значения, т.е. значения меньше нуля. Таким образом, задача сводится к решению неравенства -5с-с²<0 Решение: -5c-c²<0 (умножаем обе части неравенства на (-1), при этом знак меняется) c²+5c>0 (разложим на множители левую часть неравенства) c(c+5)>0 (далее решаем методом интервалов) + - + (-5)(0)
Т.к. знак неравенства > (больше нуля), то выбираем области, где стоит знак плюс, получаем ответ: с∈(-∞;-5)U(0;+∞)
x=![\frac{\sqrt[7]{28125} }{5}](/tpl/images/1732/6136/35464.png)
Объяснение:
0=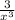 -5
-5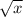
3-5x^3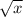 =0
=0
-5x^3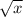 =-3
=-3
25x^6*x=9
25x^7=9
x^7=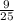
x=![\frac{\sqrt[7]{28125} }{5}](/tpl/images/1732/6136/35464.png)